出处: https://ocw.mit.edu/courses/6-050j-information-and-entropy-spring-2008/pages/compression/ 翻译: ChatGPT 英文版拆分:【拆分-Chatper3-Compression】 https://www.modevol.com/document/btcdlqe0llmwrelvuwhjmm4t
个人推荐:
【【中英双字】JPEG算法原理 jpeg图片是如何压缩的?】 https://www.bilibili.com/video/BV1TZ4y1S7iG/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5
【离散余弦变换可视化讲解】 https://www.bilibili.com/video/BV1bc411q7YG/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5
压缩
在第一章中,我们研究了信息的基本单位——比特及其各种抽象表示形式:布尔比特、逻辑电路比特、控制比特、物理比特、量子比特和经典比特。我们对改进的永无止境的追求使我们希望单个比特的表示更小、更快、更强、更智能、更安全和更便宜。
在第二章中,我们考虑了用比特数组(在这一点上是布尔比特)表示复杂对象时的一些问题。被表示的对象(符号)与用于此目的的比特数组之间的映射称为编码。我们自然希望编码更强大且更小,即,能够导致对象表示既更小又不易出错。
在本章中,我们将考虑可用于生成特别高效表示的压缩技术。在第四章中,我们将研究避免错误的技术。
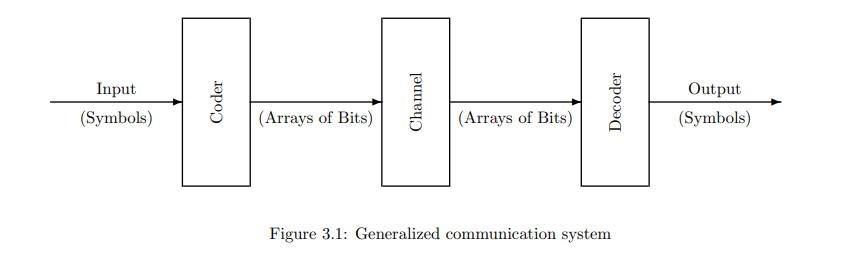
在第二章中,我们考虑了如图3.1所示的系统,其中符号被编码成比特串,这些比特串被传输(在空间和/或时间上)到解码器,解码器然后再现原始符号。
通常,同一个编码用于一个接一个的符号序列。数据压缩的作用是将表示连续符号的比特串转换为更短的比特串,以实现更经济的传输、存储或处理。其结果就是图3.2所示的系统,同时具有压缩器和扩展器。理想情况下,扩展器应完全逆转压缩器的动作,使编码器和解码器保持不变。

乍一看,这种方法似乎令人惊讶。为什么有理由相信相同的信息可以包含在更少的比特中呢?我们将看两种不同方法的压缩类型:
无损或可逆压缩(只有在原始编码效率低下时才能进行,例如有未使用的比特模式,或没有利用一些符号比其他符号使用频率更高的事实)
有损或不可逆压缩,其中原始符号或其编码表示不能从较小版本中准确重建,而是扩展器产生一个“足够好”的近似。
下面描述了六种在压缩数据文件方面非常有效的技术。前五种是可逆的,最后一种是不可逆的。每种技术都有一些特别适用的情况(最佳情况)和一些不适用的情况(最差情况)。
3.1 可变长度编码
在第二章中,我们讨论了摩尔斯电码,作为一种源编码的例子,其中英语字母表中**更频繁出现**的字母用**较短的编码词**表示,而**不太频繁出现**的字母**用较长的编码词**表示。平均而言,使用这些编码词发送的消息比所有编码词长度相同的情况要短。可变长度编码可以在源编码器或压缩器中进行。有关可变长度编码的一般过程将在第五章中给出,因此本章对此技术的讨论将延迟到那一章。
3.2 行程长度编码
假设一条消息由少数符号或字符的长序列组成。然后,该消息可以编码为符号及其出现次数的列表。例如,消息“a B B B B B a a a B B a a a a”可以编码为“a 1 B 5 a 3 B 2 a 4”。这种技术在相对少数情况下效果非常好。
一个例子是德国国旗,它可以编码为许多黑色像素、许多红色像素和许多黄色像素,这比指定每个像素要节省很多。

另一个例子来自传真技术,其中文档被扫描,长组的白色(或黑色)像素仅作为这些像素的数量传输(由于只有白色和黑色像素,甚至不需要指定颜色,因为可以假定为另一种颜色)。
行程长度编码对于没有重复序列的消息效果不佳。
例如,它可能对绘图甚至黑白扫描图像效果很好,但对照片效果不好,因为从一个像素到下一个像素的微小变化需要定义许多符号。
3.3 静态字典
如果编码有未使用的编码词,这些编码词可以分配给频繁出现的符号序列作为缩写。这样,这些序列可以用不超过单个符号所需的比特数进行编码。
例如,如果英语文本用ASCII编码并且DEL字符被视为不必要,那么将其编码词127分配给常见的单词“the”可能是有意义的。
实用的编码提供了许多这种技术的例子。编码词及其含义的列表称为编码本或字典。这里考虑的压缩技术使用的是一个静态的字典,这意味着它不会在不同消息之间变化。
一个例子可以说明这种技术。在电报之前,还有其他方案用于远距离传递消息。由威尔逊1详细描述的一种机械电报在1796年由英国海军部安装,用于在伦敦总部和普利茅斯、雅茅斯、迪尔等各港口之间通信。它由一系列小屋组成,每个小屋都能看到下一个小屋,每个小屋有六个大百叶窗,这些百叶窗可以旋转为水平(打开)或垂直(关闭)状态。见图3.4(图片因版权限制已被移除)。实际操作中,所有百叶窗都处于打开状态,直到需要发送消息时。然后,所有百叶窗都关闭以信号表示消息的开始(小屋的操作员每五分钟应查看新消息)。然后消息以一系列百叶窗模式发送,以全开模式结束。
有六个百叶窗,因此有64($26$)种模式。其中两个是控制码(全开是“开始”和“停止”,全闭是“空闲”)。其他62种模式用于字母表中的24个字母(如果包括J和U则为26个字母,但这不是必要的,因为它们是英语字母表中最近添加的),10个数字,一个词尾标记和一个页尾标记。这样就有20多种未使用的模式,被分配给常用的词或短语。特定的缩写不时变化,但包括常见的词如“the”、地点如“Portsmouth”,以及其他重要词如“French”、“Admiral”、“east”和“frigate”。还包括短语如“Commander of the West India Fleet”和“To sail, the first fair wind, to the southward”。
也许最引人注目的编码本条目是“Court-Martial to sit”和“Sentence of court-martial to be put into execution”。军事法庭真的如此常见,消息频繁到值得将64种编码模式中的两种专门用于它们吗?
正如这个例子所示,长消息可以通过一组精心选择的缩写大大缩短。然而,这有一个固有的风险:错误的影响可能更大。如果传输全文本,一个错误导致拼写错误或最坏情况下是错误的单词,人类通常可以检测并纠正。而使用缩写,一个错误的比特可能导致一个可能但非预期的含义:“east”可能变成“south”,或者一个字母可能变成“Sentence of court-martial to be put into execution”,后果严重。
这个电报系统运作良好。在一次演示中,一条消息从伦敦到普利茅斯再返回,全程500英里,仅用三分钟。这是音速的13倍。
如果使用缩写来压缩信息,则必须在发送第一条消息之前分发一本显示所有使用缩写的代码本。由于它只分发一次,所以每条消息的分发成本较低。但是,它必须被仔细构建以适应所有预期的消息,并且不能根据单个消息的需要进行更改。
这种技术对于相似度较高的信息集非常有效,就像18世纪的海军通信情况一样。它不适合更为多样化的信息。这种机械电报从未被改造为商业或公众使用,因为这会使它处理更多不同的信息集,而这些信息中没有太多共同的词语或短语。
3.4 半自适应词典
静态词典方法需要一个预先定义的词典,适用于所有消息。如果可以为每条消息定义一个新词典,压缩效果会更好,因为消息中特定的符号序列可以成为词典条目。
然而,这样做有几个缺点。首先,新的词典必须与编码消息一起传输,导致开销增加。其次,需要对消息进行分析以找到最佳的词典条目,因此在编码之前,必须对整个消息进行分析(即,这种技术有很大的延迟)。第三,计算词典的计算机需要有足够的内存来存储整个消息。
这些缺点限制了半自适应词典压缩方案的使用。
3.5 动态词典
对许多应用来说,最佳的编码方案是使用一种在处理消息时动态计算的词典,不需要与消息一起传输,并且可以在消息处理结束之前使用。乍一看,这似乎是不可能的。
然而,这样的方案确实存在,并且被广泛使用。这就是LZW压缩技术,以Abraham **L**empel、Jacob **Z**iv和Terry **W**elch命名。Lempel和Ziv实际上有一系列技术,有时被称为LZ77和LZ78,但1984年Welch的修改赋予了该技术所有期望的特性。
Welch想减少磁盘驱动器中传送到记录头的比特数量,部分是为了增加磁盘的有效容量,部分是为了提高数据传输速度。这里描述了他的方案,包括编码器和解码器。
这种技术被广泛应用于多种环境中,实现了数据的可逆压缩。应用于典型计算机的**文本文件**时,编码文件的大小通常是原文件的一半。它被用在流行的压缩产品如Stuffit或Disk Doubler中。当用于大面积相同颜色的**绘图彩色图像**时,与每个像素都存储的文件格式相比,文件大小可以减少一半以上。常用的GIF图像格式使用LZW压缩。用于颜色渐变的**照片**时,节省的空间要少得多。
由于这是一种可逆压缩技术,原始数据可以通过解码器准确重建,没有任何近似。
LZW技术似乎有许多优点。然而,它有一个主要缺点。它不是免费使用的——它是有专利的。美国专利号4,558,302于2003年6月20日到期,其他国家的专利于2004年6月到期,但在此之前,由于处理方式的问题,它引发了一场仍让许多人记忆不愉快的争议。
3.5.1 LZW专利
Welch在开发他的技术时就职于Sperry研究中心,并发表了一篇描述该技术的论文。该技术的优点很快被认可,并被应用于各种压缩方案中,包括1987年CompuServe(一个全国性的互联网服务提供商)开发的图形交换格式GIF,用于减少其计算机中图像文件的大小。
定义GIF的人并没有意识到GIF所基于的LZW算法是有专利的。Welch的文章没有警告说专利正在申请中。20世纪90年代初,万维网开始兴起,第一个图形浏览器接受了GIF图像。因此,网站开发人员通常使用GIF图像,认为这项技术属于公共领域,这也是CompuServe的意图。
到1994年,Sperry的继承公司Unisys意识到了这一专利的价值,并决定从中获利。他们找到了CompuServe,起初并未引起重视,显然他们认为这种威胁不是真的。最终,CompuServe认真对待Unisys,两家公司于1994年12月24日共同宣布,任何编写软件以创建或读取GIF图像的开发者都必须从Unisys获得许可。网站开发人员不确定他们使用GIF图像是否需要支付版税,并且对支付每个网站上每个GIF图像的费用感到不满。很快,Unisys意识到这将成为一场公关灾难,他们撤回了要求。1995年1月27日,他们宣布不会尝试收取使用现有图像或1994年底前分发的工具生成的图像的费用,但确实坚持1995年开始对图形工具进行许可。通过许可工具生成的图像可以在网络上使用而无需额外支付费用。
1999年,Unisys决定向可能包含未授权工具生成图像的个人网站收取费用,每个网站收费$5000,没有非营利组织的例外,也没有针对小型、低流量网站的较小许可费用。据报道,在最初的八个月内,只有一个网站支付了这笔费用。许多网站开发人员感到沮丧和愤怒。尽管Unisys在1995年避免了公关灾难,但在1999年却未能幸免。
自由开放的网络社区,通常愿意自由分享,与旨在赚钱的商业社区之间存在着非常明显的文化差异。
为了替代GIF,创建了一个名为PNG的无侵权公共领域图像压缩标准,但浏览器制造商对于再采用一种新的图像格式反应迟缓。而且,每个人都知道这些专利很快就会到期。除了极少数强烈感受过这场争议的人外,这场争议现在已经消失。但它仍被用来作为支持或反对专利制度变革,甚至软件专利概念的依据。
至于PNG,它提供了一些技术优势(特别是更好的透明度功能),截至2004年,几乎所有浏览器都得到了很好的支持,最显著的例外是Windows版的Microsoft Internet Explorer。
3.5.2 LZW如何工作?
编码和解码技术在第3.7节中通过一个文本示例进行了说明。
3.6 不可逆技术
本节尚未提供,抱歉。
本节将包括浮点数、JPEG 图像压缩和 MP3 音频压缩等示例。JPEG 压缩中使用的离散余弦变换(DCT)在第 3.8 节讨论。MP3 压缩的演示可在 [http://www.mtl.mit.edu/Courses/6.050/2007/notes/mp3.html](http://www.mtl.mit.edu/Courses/6.050/2007/notes/mp3.html) 查看。
3.7 LZW 压缩
下面描述了 LZW 压缩技术,并应用于两个示例中。我们将考虑编码器和解码器。LZW 压缩算法是“可逆”的,意味着它不会丢失任何信息——解码器可以精确地重建原始消息。
3.7.1 LZW 算法,示例 1
考虑对文本消息
itty bitty bit bin 进行编码和解码(这个特殊短语设计成包含重复字符串,以便字典迅速建立)。
字典条目的初始集合是 8 位字符代码,代码点为 0–255,其中前 128 个字符是 ASCII 字符,包括表 $3.1$ 中出现在上述字符串中的字符。字典条目 256 定义为“清空字典”或“开始”,257 定义为“传输结束”或“停止”。编码消息是一系列数字,这些代码代表字典条目。最初,大多数字典条目由单个字符组成,但随着消息的分析,新的条目被定义为代表两个或更多字符的字符串。结果总结在表 $3.2$ 中。


**编码算法**:定义一个位置来存放正在构建的新字典条目,并称之为 new-entry。首先将 new-entry 置为空,并发送起始代码。然后将要压缩字符串中的字符一个个地附加到 new-entry 中。一旦 new-entry 无法匹配任何现有字典条目,就将 new-entry 放入字典中,使用下一个可用的代码点,并发送不包含最后一个字符的字符串代码(此条目已在字典中)。然后使用最后接收到的字符作为下一个 new-entry 的第一个字符。当输入字符串结束时,发送 new-entry 中的代码,随后发送停止代码。就这么简单。
为了使那些喜欢将算法写成计算机程序的人受益,这个编码算法如图 $3.5$ 所示。当该过程应用于所讨论的字符串时,第一个字符是“i”,而仅包含该字符的字符串已在字典中。因此,下一字符被附加到 new-entry,结果是“it”,这不在字典中。因此,已在字典中的字符串“i”被发送,并且字符串“it”被添加到字典中,下一个可用的位置是 258。new-entry 被重置为仅包含最后一个未发送的字符,所以是“t”。接下来的字符“t”被附加,结果是“tt”,这不在字典中。该过程重复,直到字符串结束。

在开始的一段时间内,新增的字典条目都是双字符字符串,并且每遇到一个新字符就会传输一个字符串。然而,第一次遇到这些双字符字符串之一重复时,它的代码就会被发送(使用的比特数比单独发送两个字符所需的比特数更少),并定义一个新的三字符字典条目。在这个示例中,这发生在字符串“itt”上(这个消息的设计使得这种情况比在正常文本中发生得更早)。在本示例的后期,三字符字符串的代码被传输,并定义了一个四字符字典条目。
在这个示例中,代码被发送到一个接收者,期望它解码消息并输出原始字符串。接收者无法访问编码器的字典,因此解码器必须建立自己的字典副本。
**解码算法**:如果接收到起始代码,则清空字典并将 new-entry 置为空。对于下一个接收到的代码,输出该代码所代表的字符,并将其放入 new-entry 中。然后,对于后续接收到的代码,将该代码所代表的字符串的第一个字符附加到 new-entry 中,将结果插入字典中,然后输出接收到的代码所代表的字符串,并将其放入 new-entry 中以开始下一个字典条目。当接收到停止代码时,无需进行任何操作;new-entry 可以被放弃。
该算法如图 $3.6$ 所示。

请注意,编码器和解码器各自在运行时创建字典,因此字典不必显式传输,编码器可以一次性处理文本。
这是否有效,即传输所需的位数是否减少?我们在 14 次 9 位传输中发送了 18 个 8 位字符(144 位)(126 位),节省了 12.5%,这是一个非常短的示例。
对于典型的文本,字符串长度在 500 字节以下时,压缩效果不大。较大的文本文件通常可以压缩到一半,图纸的压缩效果甚至更好。
3.7.2 LZW 算法,示例 2
对文本消息进行编码和解码
itty bitty nitty grrritty bit bin (同样,这个特殊短语被设计成包含重复字符串,以便字典迅速形成;它还包含一个“三连 rrr”序列,以展示该算法的一个方面)。
字典条目的初始集合包括字符串中表 $3.3$ 中的字符,以及用于开始和停止的控制字符。

与示例 1 中使用的相同算法可以在这里应用。结果如表 $3.4$ 所示。请注意,字典构建得非常快,并且有一次传输了一个四字符的字典条目。这次压缩有效吗?绝对有效。总共发送了 33 个 8 位字符(264 位),通过 22 次 9 位传输(198 位,包括起始和停止字符),节省了 25% 的位数。

在这个示例中,有一个地方解码器需要做一些不同寻常的事情。通常,在收到传输的码字时,解码器可以在字典中查找其字符串,然后输出它,并使用其第一个字符完成部分形成的最后一个字典条目,然后开始下一个字典条目。因此,只需要一次字典查找。然而,上述算法使用了两次查找,一次用于第一个字符,另一次用于整个字符串。为什么不使用一次查找以提高效率呢?
这个示例中传输代码 271 的情况说明了一个特例,其中对应于接收到的代码的字符串尚未完整。可以找到第一个字符,但在检索到整个字符串之前,必须完成该条目。这发生在一个字符或字符串连续三次出现时,因此很少见。上述算法能正确工作,代价是额外的查找,这很少需要,可能会减慢算法的速度。只有当检测到这种情况并将其视为特例时,使用单次字典查找的更快算法才能可靠地工作。
3.8 细节:二维离散余弦变换
本节基于 Luis Pérez-Breva 于 2005 年 2 月 3 日和 Joseph C. Huang 于 2000 年 2 月 25 日的笔记。
离散余弦变换(DCT)是 JPEG(联合图像专家组)压缩算法的一个重要组成部分。DCT 用于将图像元素(像素)数组中的信息转换为一种形式,使得对人类感知最相关的信息可以被识别和保留,而不太相关的信息则可以被丢弃。
DCT 是许多用于图像压缩的离散线性变换之一。它的优点在于可以使用快速算法(与快速傅里叶变换 FFT 相关)。
描述 DCT 可以有多种数学表示法。最简洁的是使用向量和矩阵的表示法。**向量**是一维数值(或其他事物)数组。可以用一个字符表示,也可以用大方括号表示,单个元素在纵列中显示(也可以用行表示法,元素水平排列,但通常被视为向量的转置)。在这些笔记中,我们将用粗体字母($V$)表示向量。**矩阵**是二维数值(或其他事物)数组,同样可以用一个字符表示,或在大方括号中以数组形式表示。在这些笔记中,我们将用一种称为“黑板粗体”的字体($M$)表示矩阵。当需要表示向量或矩阵的**特定元素**时,使用带有一个或两个下标的符号。在**向量**的情况下,单个下标是范围从 $0$ 到 $n−1$ 的整数,其中 $n$ 是向量中的元素数量。在**矩阵**的情况下,第一个下标表示行,第二个下标表示列,每个都是范围从 $0$ 到 $n−1$ 的整数,其中 $n$ 是行数或列数,只有当矩阵是方阵时,它们才相同。
3.8.1 离散线性变换
一般而言,离散线性变换以向量为输入并返回相同大小的另一个向量。输出向量的元素是输入向量元素的线性组合,因此可以通过矩阵乘法来实现这种变换。
例如,考虑以下矩阵乘法:
如果将此方程中的向量和矩阵命名为
那么方程$(3.1)$ 变为
我们现在可以将 $C$ 视为一个离散线性变换,它将输入向量 $I$ 变换为输出向量 $O$。顺便说一下,这个特定的变换 $C$ 将输入向量 $I$ 变换为一个包含其分量的*和*(5)和*差*(3)的向量。
对于作用于 3 元素向量的 3×3 矩阵,过程相同:
这也可以写成简洁的形式
此时,向量的大小为 3,矩阵为 3×3。
一般而言,对于这种形式的变换,如果矩阵 $C$ 有逆矩阵 $C−1$,则可以通过以下方式从其变换中重建向量 $I$:
方程 $(3.3)$ 和 $(3.1)$ 说明了当输入为列向量时的线性变换。对于行向量,过程类似,但向量和矩阵的顺序颠倒,并且变换矩阵转置。这种变化与将行向量视为列向量的转置是一致的。例如:
**向量**在处理具有**一维**特性的对象(例如有限次采样的**声音**波形)时非常有用。**图像**本质上是**二维**的,因此使用**矩阵**来表示像素的属性是很自然的。**视频**本质上是**三维**的(两个空间维度和一个时间维度),因此使用**三维数组**来表示它们的数据是很自然的。这里给出的简洁的向量-矩阵表示法可以优雅地扩展到二维系统,但不能扩展到更高维度(可以使用其他数学表示法)。
将线性变换扩展为作用于矩阵(而不仅仅是向量)并不困难。
例如,考虑一个只有六个像素的非常小的图像,每行三个像素,共两列。表示每个像素某些属性(例如其亮度在 0 到 1 之间)的数值可以形成一个 3×2 的矩阵:
导致 3×2 输出矩阵的一般线性变换需要 36 个系数。当矩阵中的元素排列反映所表示的基础对象时,一组较不一般的线性变换可能有用,这些变换分别作用于行和列,使用不同的矩阵 $C$ 和 $D$:
或,用矩阵表示法,
请注意,这种情况下左边的矩阵 $C$ 和右边的矩阵 $D$ 通常大小不同,且可能具有不同的一般特性。(一个重要的特例是 $I$ 为方阵,即它包含相同数量的行和列。在这种情况下,输出矩阵 $Q$ 也是方阵,并且 $C$ 和 $D$ 大小相同。)
3.8.2 离散余弦变换
在线性代数的语言中,公式
表示将矩阵 $X$ 变换为系数矩阵 $Y$。假设变换矩阵 $C$ 和 $D$ 分别有逆矩阵 $C−1$ 和 $D−1$,则可以通过逆变换从系数中重建原始矩阵:
这种将 $Y$ 解释为用于重建 $X$ 的系数的方式在离散余弦变换中特别有用。
离散余弦变换是一种上述类型的离散线性变换:
其中所有矩阵都是 $N×N$ 大小的,并且两个变换矩阵互为转置。该变换之所以称为余弦变换,是因为矩阵 $C$ 定义为
其中 $m,n=0,1,…(N−1)$。这个矩阵 $C$ 有一个等于其转置的逆矩阵:
使用方程 $3.12$ 和方程 $3.13$ 中定义的 $C$,我们可以计算任意矩阵 $X$ 的 DCT $Y$,其中矩阵 $X$ 可以表示给定图像的像素。在 DCT 的背景下,方程 $3.11$ 中概述的逆过程称为逆离散余弦变换(IDCT):
通过这个方程,我们可以计算 DCT 的基矩阵集,即:每个 $Y$ 元素对应的矩阵集。让我们构造所有可能的图像集,每个图像仅有一个非零像素。这些图像将代表矩阵 $Y$ 的各个系数。

回顾我们上面关于离散线性变换的概述,如果我们想从其 DCT $Y$ 中恢复图像 $X$,只需将 $Y$ 的每个元素与图 $3.7(b)$ 中对应的矩阵相乘即可。实际上,图 $3.7(b)$ 引入了 DCT 基的一个非常显著的特性:它编码了空间频率。通过忽略具有较小 DCT 系数的空间频率,可以实现压缩。想象棋盘的图像——它具有高空间频率成分,几乎所有低频成分都可以去除。相反,模糊图像往往具有较少的高空间频率成分,然后可以将图 $3.7(b)$ 右下角的高频成分设为零,作为“可接受的近似”。这就是 JPEG 背后不可逆压缩的原理。
图 $3.8$ 显示了用于生成上述 4×4、8×8 和 16×16 DCT 基图像的 MATLAB 代码。

麻省理工学院开放课程资源 [http://ocw.mit.edu](http://ocw.mit.edu/)
6.050J / 2.110J 信息与熵 2008 春季课程
有关引用这些材料的信息或我们的使用条款,请访问:[http://ocw.mit.edu/terms](http://ocw.mit.edu/terms)。