出处: https://ocw.mit.edu/courses/6-050j-information-and-entropy-spring-2008/pages/noise-errors/
翻译: ChatGPT
英文版拆分: 【拆分-Chapter4-Errors】 https://www.modevol.com/document/iqbi4z5nxg5gxgprkggle65a
个人推荐:
How to compute the Hamming distance: https://youtu.be/P02mJhS9qQ4?si=l3H_FFKUaFpqWLAd
【【官方双语】汉明码Pa■t1,如何克服噪■】 https://www.bilibili.com/video/BV1WK411N7kz/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5
【信用卡号校验【Luhn(模10)算法及另外一种隐藏的方法】】 https://www.bilibili.com/video/BV1eU4y1E7M2/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5
【简单了解国际标准书号ISBN】 https://www.bilibili.com/video/BV1He4y1f77W/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5
ISBN number check digit: https://youtu.be/5qcrDnJg-98?si=xApusaY50NkWouh9
第四章 错误
在第二章中,我们看到了一些如何用比特数组表示符号的例子。在第三章中,我们研究了一些压缩这些符号的比特表示或一系列此类符号的方法,以便需要更少的比特来表示它们。如果在保留所有原始信息的同时进行压缩,则这种压缩被称为无损或可逆的,但如果在丢失(可能不重要的)信息的情况下进行压缩,则这种压缩被称为有损或不可逆的。源编码和压缩通常结合成一个操作。
由于压缩,携带相同信息的比特减少了,因此每个比特变得更加重要,而单个比特错误的后果也更加严重。所有实际系统都会在处理信息时引入错误(当然有些系统比其他系统更多)。在本章中,我们将研究确保这种不可避免的错误不会造成危害的技术。
4.1 系统模型的扩展
我们的信息处理模型将扩展为包括“信道编码”。新的信道编码器会向消息添加比特,这样如果消息在某种程度上受到损坏,信道编码器将能够知道,甚至可能能够修复损坏。

4.2 错误是如何发生的?
上图所示的模型是相当通用的,因为其目的可能是将信息从一个地方传输到另一个地方(通信),将其存储以供以后使用(数据存储),或甚至处理它,使输出不必是输入的真实复制品(计算)。
不同的系统涉及不同的物理设备作为信道(例如通信链路、软盘或计算机)。许多物理效应都可能导致错误。CD或DVD可能会被划伤。内存单元可能会失效。电话线路可能会有噪音。计算机门可能会对电源电压的意外突升作出反应。
为了我们的目的,我们将所有这些错误建模为一个或多个比特从1变为0或反之亦然的变化。
在通常情况下,一条消息由多个比特组成,我们通常假设不同的比特独立地受到损坏,但在某些情况下,相邻比特的错误不是相互独立的,而是具有共同的潜在原因(即错误可能成簇发生)。
4.3 检测与纠正
处理错误有两种方法。一种是检测错误,然后让使用输出的人或系统知道发生了错误。另一种是让信道解码器尝试通过纠正错误来修复消息。
在这两种情况下,都会向消息中添加额外的比特,使其变得更长。结果是消息包含冗余——如果没有冗余,每种可能的比特模式都是一个合法消息,而错误只会将一个有效消息变成另一个有效消息。通过改变设置,使许多(事实上,大多数)比特模式不对应合法消息,错误的效果通常是将消息更改为非法模式之一;信道解码器可以检测到错误并采取适当的行动。事实上,如果每个非法模式在某种意义上(将在下文描述)比任何其他模式更接近一个合法消息,解码器可以替换最接近的合法消息,从而修复损坏。
在日常生活中,错误检测和纠正是常见的。书面和口头交流使用的是自然语言,如英语,这些语言有足够的冗余(估计为50%),即使省略了几个字母、声音,甚至单词,人们仍然能理解消息。
注意,信道编码器由于添加比特到模式中,通常会保留所有原始信息,因此是可逆的。信道通过允许错误发生,实际上引入了信息(即具体哪些比特被更改的细节)。解码器是不可逆的,因为它会丢弃一些信息,但如果设计良好,它会丢弃由错误引起的“坏”信息,并保留原始信息。在后续章节中,我们将定量分析这种系统中的信息流。
4.4 汉明距离
我们需要一种技术来描述两个比特模式的相似程度。在物理量(如长度)的情况下,认为两个测量值很接近或大致相等是很自然的。那么,两个比特模式是否也有类似的接近感呢?
起初,可能会认为如果两个比特模式表示的是相邻的整数或接近的浮点数,那么它们就是接近的。然而,这种概念并不实用,因为它基于赋予比特模式的特定含义。两个比特模式在第一个比特上的差异是否比在最后一个比特上的差异更大或更小,这并不明显。
一个更有用的定义是两个比特模式之间不同比特的数量。这被称为汉明距离,以理查德·W·汉明(1915 - 1998)[^1]的名字命名。因此,0110和1110之间的汉明距离为1。两个相同的模式之间的汉明距离为0。
注意,汉明距离只能在两个具有相同数量比特的比特模式之间定义。谈论单个比特串的汉明距离或两个不同长度的比特串之间的汉明距离是没有意义的。
使用这个定义,可以通过输入信道和输出信道的两个比特模式之间的汉明距离来描述信道中引入的错误的影响。没有错误意味着汉明距离为0,单个错误意味着汉明距离为1。如果发生两个错误,通常意味着汉明距离为2。(然而,注意如果两个错误发生在同一个比特上,第二个错误会抵消第一个错误,实际汉明距离为0。)
编码器的作用也可以用汉明距离来理解。为了提供错误检测,编码器必须生成比特模式,使得任何两个不同输入在输出中的汉明距离至少为2——否则,单个错误可能会将一个合法码字转换为另一个合法码字。为了提供双重错误保护,任何两个有效码字的间隔必须至少为3。为了可能进行单错误纠正,所有有效码字之间的汉明距离必须至少为3。
4.5 单个比特
单个比特的传输可能看起来不重要,但它确实引出了常用的一些错误检测和纠正技术。
保护单个比特的方法是多次发送,并期望每次发送的比特大多数情况下保持不变。最简单的情况是发送两次。因此,信道编码器将消息0替换为00,将消息1替换为11。如果两个比特不同,解码器就会发出警报(这只能是由于错误造成的)。但是这里有一个微妙的问题。如果有两个错误会怎样?如果两个错误都发生在同一个比特上,那么该比特将恢复到其原始值,就好像没有发生错误一样。但如果两个错误发生在不同的比特上,那么它们最终会相同,尽管是错误的,并且错误未被检测到。如果有更多的错误,那么未检测到的变化的可能性就会显著增加(奇数错误会被检测到,但偶数错误不会)。
如果多重错误的可能性较高,更大的冗余可以提供帮助。因此,为了检测双重错误,可以将单个比特发送三次。除非信道解码器接收到的三个比特都相同,否则就知道发生了错误,但不知道可能有多少错误。当然,三重错误可能未被检测到。
那么如何让解码器不仅检测到错误,还能纠正错误呢?如果已知最多只有一个错误,并且单个比特被发送三次,那么信道解码器可以判断是否发生了错误(如果三个比特不完全相同),并且还可以判断原始值是什么——这种过程有时被称为“多数逻辑”(选择出现次数最多的比特)。这种技术被称为“三重冗余”,可用于保护通信信道、内存或任意计算。
注意,三重冗余可以用来纠正单个错误或检测双重错误,但不能同时做到这两点。如果需要两者,可以使用四重冗余——发送四个相同的比特副本。
图 **4.2** 和图 **4.3** 说明了三重冗余如何保护单个错误,但如果存在两个错误则可能失效。

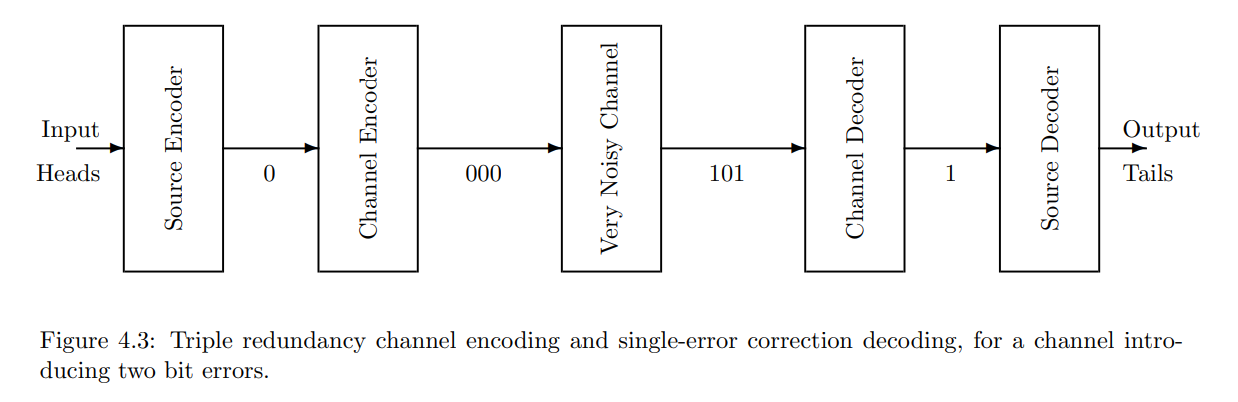
两个重要的问题是这些技术的效率和效果。
关于效率,方便的定义**码率**为信道编码前的比特数除以编码器之后的比特数。因此码率介于0和1之间。双重冗余的码率为0.5,三重冗余为0.33。
关于效果,如果错误的可能性非常小,忽略更不可能发生的两个错误如此接近的情况可能是合理的。如果是这样,三重冗余是非常有效的。另一方面,一些物理错误源可能会在大范围内消除数据(比如CD上的物理划痕),在这种情况下,一个错误,即使不太可能发生,也可能伴随着相邻比特的类似错误,因此三重冗余将无效。
4.6 多个比特
为了检测一系列比特中的错误,可以使用多种技术。有些技术不仅可以进行错误检测,还能进行错误纠正。
4.6.1 奇偶校验
考虑一个字节,即8个比特。为了检测单个错误,可以添加一个“奇偶校验”位(也称为“校验位”),将8比特字符串变为9比特。如果比特中1的数量是奇数,则添加的比特为1,否则为0。这样,9比特字符串中1的数量总是偶数。解码器只需计算1的比特数,如果是奇数,则知道存在错误(或者更一般地说,有奇数个错误)。
解码器无法修复损坏,甚至无法确定损坏是否可能发生在奇偶校验位上,如果是这样,数据比特仍然是正确的。它也无法检测到双重错误(或更一般地说,偶数个错误)。使用奇偶校验位的效率较高,因为码率为8/9,但其效果有限。它无法处理信道表示计算的情况,因此输出不打算与输入相同。它最常用于错误发生可能性非常小,并且没有理由认为相邻比特的错误会一起发生,接收方能够请求数据重传的情况。
有时,即使无法重传,也会使用奇偶校验。在早期的IBM个人计算机上,内存引用通过单比特奇偶校验进行保护。当检测到错误时(非常罕见),计算机会崩溃。
错误纠正比错误检测更有用,但需要更多比特,因此效率较低。接下来讨论两种较为常见的方法。
如果传输的数据更方便地被认为是由多个比特编码的对象序列(例如字母或数字),可以通过添加类似对象而不是奇偶校验位来实现奇偶校验位的优势。例如,可以在数字数组中添加**校验位**。第 **4.9** 节讨论了一些校验位的常见用法。
4.6.2 矩形码
矩形码可以同时提供单错误纠正和双错误检测。假设我们希望保护一个字节的信息,即八个数据比特 $D0$ $D1$ $D2$ $D3$ $D4$ $D5$ $D6$ $D7$。我们将这些比特排列在一个矩形表中,并为两行和四列添加奇偶校验位:

其中每个奇偶校验位 $PR0$ $PR1$ $PC0$ $PC1$ $PC2$ $PC3$ 被设置为相应行或列的总奇偶校验为偶数。总奇偶校验位 $P$ 设置为右列(仅由奇偶校验位组成)的奇偶校验为偶数——这保证了底行的奇偶校验也是偶数。
这15个比特可以通过信道发送,解码器分析接收到的比特。它对三行和五列共八个奇偶校验进行检查。如果任意一个比特有单个错误,那么三行中的一个和五列中的一个奇偶校验将是错误的。由此可以识别出出错的比特(它位于奇偶校验错误的行和列的交点)并进行修改。
如果有两个错误,会出现不同的奇偶校验失败模式;双重错误可以被检测到但不能被纠正。三重错误可能更棘手,因为它们可能模仿无辜比特的单错误。
其他几何灵感的编码也可以被设计出来,基于将比特排列成三角形、立方体、金字塔、楔形或更高维的结构。
4.6.3 汉明码
假设我们希望纠正单个错误,并且愿意忽略多个错误的可能性。理查德·汉明发明了一组代码,使用最少数量的额外奇偶校验位来实现这一目的。
信道编码器添加的每一个额外比特允许解码器进行一次奇偶校验,从而提供一个位的信息,用于帮助识别错误的位置。
例如,如果使用三个额外比特,这三个测试可以识别多达八种错误情况。其中一种情况是“无错误”,因此剩下七种情况用于识别多达七个位位置上的错误。这样,数据块可以有七个比特长。其中三个比特用于错误检查,剩下四个用于有效载荷数据。
同样地,如果有四个奇偶校验位,数据块可以是15个比特长,剩下11个用于有效载荷。
在给定数量的奇偶校验位的情况下,尽可能大的有效载荷的代码有时被称为“完美”代码。当然,也可以有较小的有效载荷,在这种情况下,得到的汉明码的码率会较低。例如,由于大部分数据处理集中在字节上,每个字节八个比特,一个方便的汉明码是使用四个奇偶校验位来保护八个数据比特。因此,可以处理两个字节的数据,加上奇偶校验位,正好是三个字节。
表 **4.2** 列出了一些汉明码。没有显示1个奇偶校验位的简单情况,因为没有数据空间。第一个条目是一个简单的例子,我们已经见过了。它是三重冗余,其中一个数据比特发送一个三比特块。正如我们之前看到的,这种方案能够进行单错误纠正或双错误检测,但不能同时进行(这对于所有汉明码都适用)。第二个条目非常有趣,因为它是一个效率合理的最简单的汉明码。

让我们设计一个 (7, 4, 3) 汉明码。有几种方法可以做到这一点,但从解码器开始可能是最简单的。解码器接收七个比特,并对这些比特组进行三次奇偶校验,目的是识别错误发生的位置。如果结果都是偶数奇偶校验,解码器认为没有错误发生。否则,通过知道哪些奇偶校验操作失败来推断更改的比特的身份。在有三个奇偶校验位的完美汉明码中,有一个特别优雅:
第一次奇偶校验使用比特 4, 5, 6 或 7,因此如果其中一个发生变化则失败
第二次奇偶校验使用比特 2, 3, 6 或 7,因此如果其中一个发生变化则失败
第三次奇偶校验使用比特 1, 3, 5 或 7,因此如果其中一个发生变化则失败
这些规则很容易记住。三个奇偶校验是故障比特位置的二进制表示的一部分——例如,整数6的二进制表示为110,对应于第一和第二次奇偶校验失败,而第三次没有失败。
现在考虑编码器。这七个比特中,有四个是原始数据,三个是由编码器添加的。如果原始数据比特是 3, 5, 6, 7,那么编码器根据上述规则计算比特 1, 2, 4 是很容易的——例如,比特2被设置为使比特 2, 3, 6, 7 的奇偶校验为偶数所必需的值,这意味着如果比特 3, 6, 7 的奇偶校验已经是偶数,则为0,否则为1。编码器计算奇偶校验位并按所需顺序排列所有比特。然后,解码器在必要时纠正比特后,可以提取数据比特并丢弃奇偶校验位,奇偶校验位已经完成了它们的工作,不再需要。
4.7 块码
在某些数据量上提供纠错保护,然后将结果发送为长度为 $n$ 的块,这种方法是很方便的。如果该块中的数据比特数为 $k$,那么奇偶校验位的数量为 $n−k$,这种编码通常称为 $(n,k)$ 块码。因此,刚刚描述的汉明码是 $(7,4)$。
习惯上(我们在这些笔记中也会这样做),括号内还包括任意两个有效码字或原始数据项之间的最小汉明距离 $d$,形式为 $(n,k,d)$。刚才描述的汉明码可以分类为 $(7,4,3)$ 块码。
4.8 高级编码
具有大于3的最小汉明距离的块码是可能的。它们可以处理多个错误。其中一些被称为Bose-Chaudhuri-Hocquenhem(BCH)码。今天非常有商业兴趣的一类编码是1960年由麻省理工学院林肯实验室的Irving S. Reed和Gustave Solomon宣布的。这些编码处理的是字节数据而不是比特。用于CD播放器的(256, 224, 5)和(224, 192, 5)Reed-Solomon码可以一起防护长时间错误突发。
更先进的信道编码不仅使用当前数据块,还利用过去的数据块。此类编码的编码器和解码器需要局部存储,但不一定需要很多。此类高级编码的数据处理可能非常具有挑战性。开发一种高效、能防护大量错误、易于编程且执行迅速的编码并不容易。一类重要的编码被称为卷积编码,其中一个重要的子类是网格编码,常用于数据调制解调器。
4.9 细节:校验位
错误检测通常用于减少人为错误。许多人需要处理长串的序列号或字符序列,这些序列会被大声读出或在键盘上输入。例如,信用卡号码、社会保障号码和软件注册码。这些操作容易出错。可以包含额外的数字或字符来检测错误,就像在比特串中包含奇偶校验位一样。这通常是足够的,因为当检测到错误时,可以方便地重复操作。
在其他情况下,例如电话号码或电子邮件地址,不使用校验字符,因此任何序列可能都是有效的。显然,使用这些时必须更加小心,以避免拨错号码或将电子邮件或传真发送给错误的人。
信用卡
信用卡号码有一个额外的**校验位**,其计算方式由IBM的H.P. Luhn在1954年规定。该算法旨在防止一种常见错误,即相邻两个数字的调换。
信用卡号码通常包含15或16位数字(Luhn算法实际上适用于任何位数)。前六位数字表示发卡组织。金融行业不鼓励公开这些代码,尽管大多数已经广为人知,尤其是那些认真考虑欺诈的人。这六位中的第一位表示与该卡关联的经济部门,例如1和2表示航空公司,3表示旅游和娱乐,4、5和6表示银行和商店。最后一位是校验位,其他数字表示个人卡账户。
信用卡发行者根据这一方案被分配了自己的前缀。例如,American Express卡以34或38开头,Visa卡以4开头,MasterCard卡以51、52、53、54或55开头,Discover卡以6011或65开头。
Luhn算法测试信用卡号码(包括校验位)是否有效。**首先**,从卡号中选择交替位置出现的数字,从倒数第二位开始。例如,如果卡号是1234 4567 7891,则这些数字是9、7、6、4、3和1。注意这些数字中有多少个大于4(在本例中是3个)。**然后**将这些数字相加(例如,9 + 7 + 6 + 4 + 3 + 1 = 30)。**再**将卡号中的所有数字相加(在本例中是57)。查看这三个数字的总和(在本例中是3 + 30 + 57 = 90)。如果结果是10的倍数,如本例所示,则该卡号通过测试,可能是有效的。否则,它是无效的。
该方法检测所有单一数字错误,几乎所有相邻数字的调换错误(例如将“1234”输入为“1243”),但无法捕捉许多其他可能的抄写错误,例如将“1234”输入为“3412”。它具有较高的码率(仅对14或15个有效载荷数字添加一个校验位),且使用简单。它不能用于纠正错误,因此只能在使用其他手段进行纠正的情况下有价值。
ISBN
国际标准书号 (ISBN) 是一个13位数字的编号,用于唯一标识一本书或类似书的东西。相同书的不同版本可能有不同的ISBN。书可以是印刷版,也可以是电子书、音频磁带或软件。ISBN对消费者来说意义不大,但对书商、图书馆、作者、出版商和发行商来说非常有用。
该系统由英国书商W.H. Smith在1966年使用9位数字创建,1970年升级为国际使用,通过在现有编号前加0,并在2007年升级为13位数字,通过在现有编号前加978并重新计算校验位。
书的ISBN显示在“ISBN”字母后,通常在书籍封皮背面或平装书的封底。通常它靠近一些条形码,并且经常以机器可读的字体呈现。
ISBN有五部分(2007年之前为四部分),长度可变,由连字符分隔。首先是前缀978(2007年之前缺失)。当使用该前缀的号码用完时,将使用前缀979。接下来是国家识别码(或共享一种语言的国家或地区组)。然后是特定出版商的编号。然后是书名的识别码,最后是单个校验位。国家识别码由位于柏林的国际ISBN机构分配。出版商识别码在所代表的国家或地区内分配,书名识别码由出版商分配。校验位按以下所述计算。
例如,考虑ISBN 0-9764731-0-0(这是2007年之前的格式)。语言区域代码0表示英语国家。出版商9764731是麻省理工学院电气工程和计算机科学系。项目识别码0表示书籍《The Electron and the Bit》。标识符0的结果是因为这是该出版商使用ISBN出版的第一本书。使用7位数字标识出版商,仅使用1位标识项目反映了这是一个非常小的出版商,可能不需要超过10个ISBN。ISBN可以成套购买,10个(2007年为269.95美元),100个(914.95美元),1000个(1429.95美元)或10000个(3449.95美元),在购买时分配的出版商识别码分别为7、6、5或4位。这种安排方便了许多小出版商和少数大出版商。
出版趋势更倾向于许多小出版商而不是少数大出版商,这可能会给ISBN系统带来压力。小出版商必须至少一次购买10个号码,如果只出版了一两本书,未使用的号码不能被另一个出版商使用。主要不是出版商但偶尔出版一本书的组织可能会因为没人记得它们最后放在哪里而丢失未使用的ISBN。
2007年及之后出版的书籍有13位ISBN,设计为与商店广泛使用的通用产品代码 (UPC) 条形码兼容。用于13位ISBN的UPC校验位查找程序如下:从12位数字(不包括校验位)开始。将第一、第三、第五及其他奇数位置的数字相加并将和乘以3。然后将结果加到偶数位置的数字和上(2、4、6、8、10和12)。将结果从下一个更高的10的倍数中减去。结果是0到9之间的一个数字,即所需的校验位。
此技术生成了一个大码率(0.92)的代码,可以捕捉所有单数字错误,但不能捕捉所有相邻数字的调换错误。
对于2007年之前出版的书籍,校验位可以通过以下程序计算。从九位数字(不包括校验位)开始。将每一位乘以其位置,最左边的位置为1,最右边的位置为9。将这些乘积相加,并找到和的模11的余数(即需要减去的数以使结果成为11的倍数)。结果是0到10之间的一个数字。这就是校验位。例如,对于ISBN 0-9764731-0-0,1 × 0 + 2 × 9 + 3 × 7 + 4 × 6 + 5 × 4 + 6 × 7 + 7 × 3 + 8 × 1 + 9 × 0 = 154,模11为0。
如果校验位小于10,则在ISBN中使用。如果校验位是10,则使用字母X(这是罗马数字十)。如果你查看几本书,你会发现偶尔会看到校验位X。
此技术生成了一个大码率(0.9)的代码,能够有效检测两个相邻数字的调换或任意单个数字的更改。
ISSN
国际标准连续出版物号 (ISSN) 是一个8位数字的编号,用于唯一标识印刷或非印刷的连续出版物。ISSN以“ISSN 1234-5678”的形式出现在每期连续出版物中。公众通常不注意这些编号,但它们对出版商、发行商和图书馆非常有用。
ISSN用于报纸、杂志和许多其他类型的期刊,包括学术期刊、学会交易、专著系列,甚至博客。ISSN适用于整个系列,预期将无限期继续,而不是单个期刊。分配是永久性的——如果期刊停止出版,ISSN不会被回收,如果期刊更名,则需要新的ISSN。在美国,ISSN由国会图书馆的一个办公室免费逐个分配。
与ISBN不同,ISSN的各部分没有关联的意义,除了前七位数字组成一个唯一编号,最后一位是校验位。除非格式更改,否则最多可以分配10,000,000个ISSN。截至2006年,全球已分配了1,284,413个,其中包括当年发行的57,356个。
校验位按以下步骤计算。从七位数字(不包括校验位)开始。将每位数字乘以其(反向)位置,最左边的位置为8,最右边的位置为2。将这些乘积相加,并从下一个更高的11的倍数中减去。结果是0到10之间的一个数字。如果小于10,则该数字是校验位。如果等于10,则校验位为X。校验位成为最终ISSN的第八位数字。
MIT OpenCourseWare [http://ocw.mit.edu](http://ocw.mit.edu/)
6.050J / 2.110J 信息与熵 2008年春季
有关引用这些材料或使用条款的信息,请访问:[http://ocw.mit.edu/terms](http://ocw.mit.edu/terms)。