错误纠正

爱丽丝和鲍勃发现了一个惊人的技巧。他们通过拉动一根电线，硬或软地传输 0 和 1 来交换消息。然而，由于阵风的影响，在传输过程中可能会出现错误的零或一。然而他们已经找到了一种在噪声存在的情况下进行无误传输的方法。他们是如何做到的呢？

在1940年代，理查德·哈明在贝尔实验室遇到了类似的问题。理查德：在贝尔电话实验室，我们大约有10%的实验是在计算机上进行的，而约90%的实验是在实验室进行的。我期待着，随着时间的推移，我们将有90%的实验在计算机上进行，而只有10%在实验室进行。速度、成本和工作量都倾向于计算机而不是实验室方法。

当时，计算机使用打孔卡片来存储信息，用孔和无孔来表示1和0。这个系统容易出错，因为卡片常常会弯曲或打孔错误。因此，孔可能会被忽略，或者无意中会打孔，导致位翻转。这些错误会导致整个系统停止，直到手动找到错误位置并进行纠正为止。

哈明自己想出了一种方法，可以自动检测和纠正单比特错误，而不会中断计算。他的解决方案根植于重复的直观思想，当我们面对干扰时，或者我们的消息有可能被损坏时，我们都会采取的措施。

他的纠错码建立在奇偶校验位的简单概念上。奇偶校验位是一位单独添加到消息末尾的位，指示消息中1的数量是偶数还是奇数。如果发生单个错误，接收器就可以检测到它，因为奇偶校验位将不再匹配。

然而，为了检测和纠正单个错误，哈明需要添加更多的奇偶校验位来识别错误位置。这导致了他的七-四码，它将**三个奇偶校验位**添加到每个**四位数据位块**中，如下所示。

首先，我们从三个奇偶校验位开始，可以用一个圆表示。这些圆相交产生四个区域。将四个数据位按特定顺序放置在这些区域内。为了计算奇偶校验位，我们逐个检查每个圆，每个圆包含三个数据位。我们像以前一样确定奇偶校验位。对数据位进行求和，如果得到零或两个，则奇偶校验位为偶数为零，如果得到一个或三个，则奇偶校验位为奇数为一。我们对所有圆执行此操作，最终得到与四个数据位匹配的三个奇偶校验位。


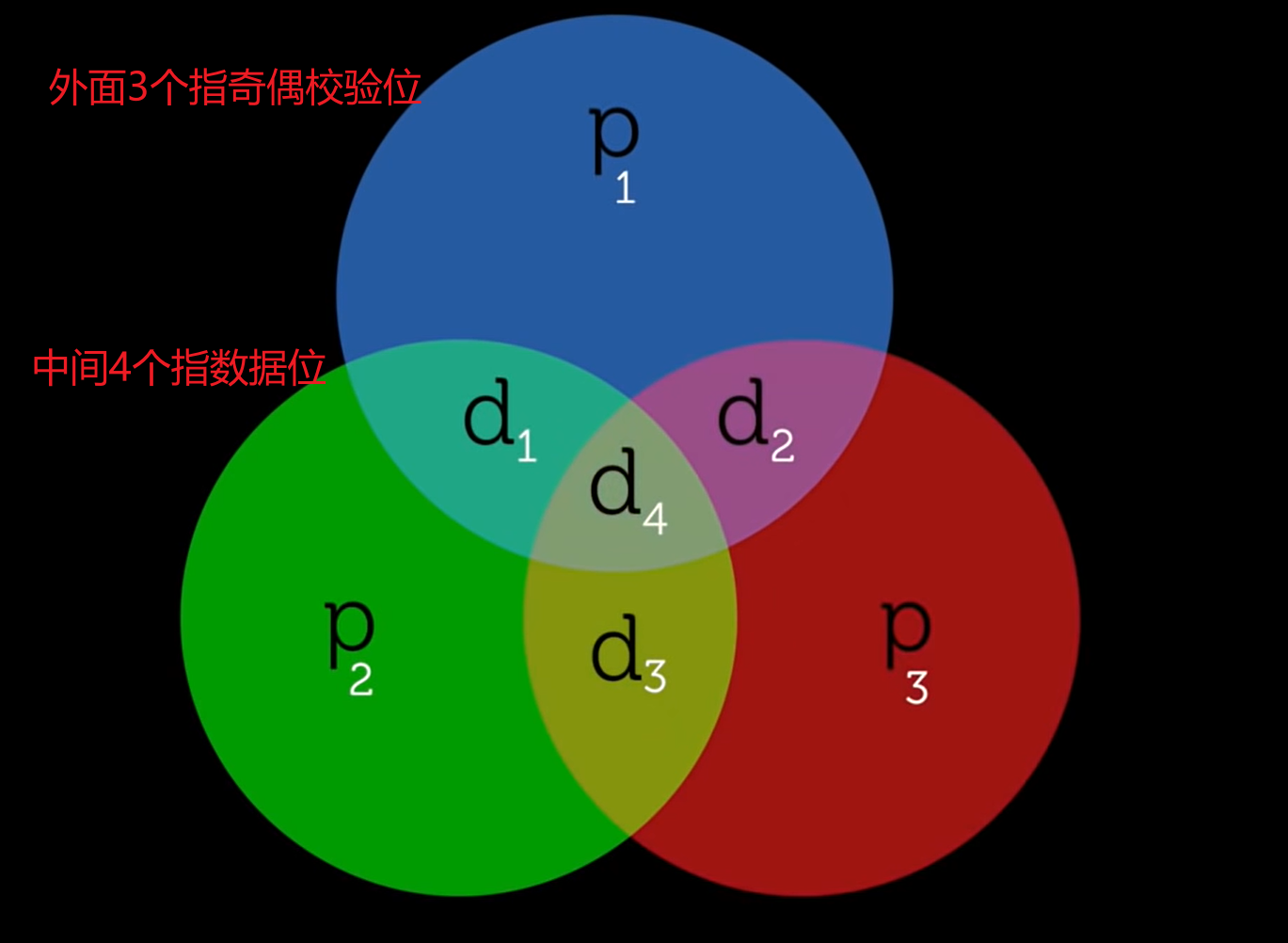
然后，这些位按照标准顺序放置如下： P1 D1 P2 D2 P3 D3 D4 （P是指奇偶校验位 parity bits，D是指数据位 data bits ）

现在请注意，这个系统可以通过一个简单的规则自动纠正单个错误。如果发生单个错误，则两个或更多的奇偶校验位将是不正确的，它们相交的位置就是错误的位置。然后，该相交数据位将自动翻转，以使所有奇偶校验位再次有效。这就是爱丽丝和鲍勃的技巧。

额外的奇偶校验位被称为冗余位，因为它们不携带任何新信息。所有纠错码都是这样工作的。它们都稍微增加了源消息的大小，以自动纠正错误为代价。

我们还将纠错码用于存储，例如在物理CD上，信息使用特殊的代码编码，以纠正由划痕或灰尘引起的错误块，这些错误块会损坏存储在表面上的长序列的零和一。这就是为什么你可以划伤CD，它通常仍然可以完美播放的原因。

克劳德·香农利用这种冗余的思想重新定义了通信通道的容量，因为随着通道上的噪声增加，我们必须增加冗余量来进行无误通信。这必然会减少每单位时间内可以发送的有效信息量。