信息熵
想象两台机器。它们都输出字母A、B、C或D的消息。
机器一随机生成每个符号,它们都以$25%$的概率发生,
而机器二根据以下概率生成符号(A是$50%$,B是$12.5%$,C是$12.5%$,D是$25%$)。
哪台机器产生的信息更多?
克劳德·香农巧妙地重新表达了这个问题:如果你必须从每台机器预测下一个符号,你期望问的最少数量的`是或否`问题?
让我们看看机器一。最有效的方法是提出一个问题将可能性分成两半。例如(以答案为`B`为例),我们的第一个问题,我们可以问是否是任何两个符号,比如`“是A或B吗?”`,因为A或B有50%的机会和C或D有50%的机会。得到答案后,我们可以消除一半的可能性,然后我们将剩下两个符号,两者同样可能。所以我们只需选择一个,比如`“是A吗?”`,在这第二个问题之后,我们将正确地识别符号。
flowchart TD
A[Is it AB?] --> |Yes|B[Is it A?]
A --> |No |C[Is it C?]
B --> |Yes|E(A)
B--> |No|F(B)
C --> |Yes|G(C)
C --> |No|H(D)由此我们可以说,机器一的不确定性是每个符号$2$个问题。或者说,对于机器一,我们可以通过问$2$个问题来确定下一个符号。
那机器二呢?这一次,每个符号的概率是不同的,所以我们提问的方式是不同的。
$$P(A)=0.50,P(B)=0.125,P(C)=0.125,P(D)=0.25$$
这里A有50%的发生概率,其他所有字母加起来为50%。我们可以从问`“是A吗?”`开始,如果是A,我们就完成了,在这种情况下只有一个问题。否则,我们剩下两个相等的结果,D或,B和C。我们可以问,`“是D吗?”`。如果是,我们用两个问题完成。否则,我们必须问第三个问题来确定最后两个符号中的哪一个。
flowchart TD
A[Is it A?] --> |Yes|B(A)
A --> |No| C[Is it D?]
C --> |Yes| D(D)
C --> |No| E[Is it C?]
E --> |Yes| F(C)
E --> |No | G(B)平均来说,你期望问多少问题确定一个来自机器二的符号?
扔一个圆盘下来,根据圆盘落地的位置,我们输出A、B、C或D。
机器一:
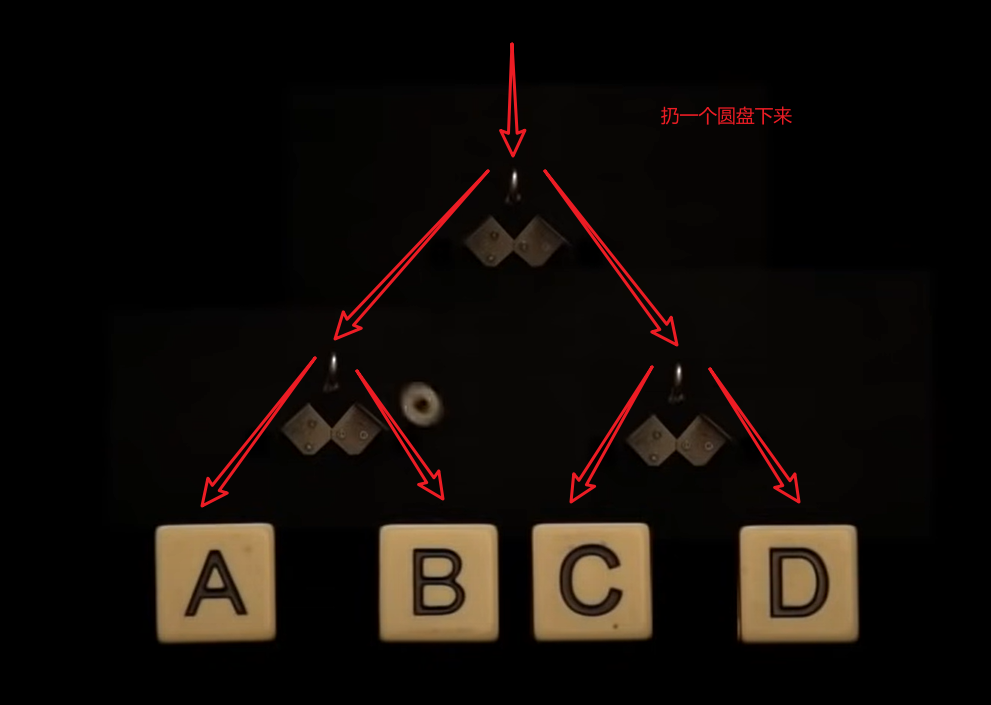
机器二:
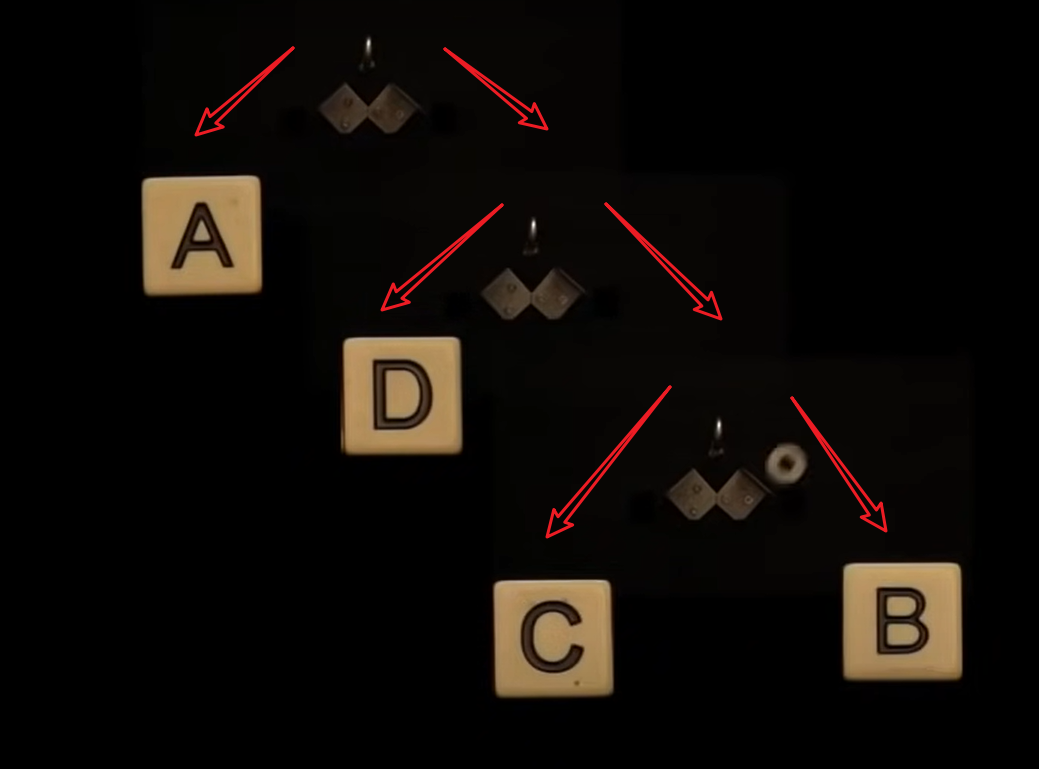
我们现在只需要计算加权平均值。预期的弹跳次数是,符号A的概率乘以一次弹跳,加上符号B的概率乘以三次弹跳,加上符号C的概率乘以三次弹跳,加上符号D的概率乘以两次弹跳。这计算出为1.75次弹跳。
$$#弹跳次数=PA×1+PB×3+PC×3+PD×2$$ $$#弹跳次数=0.5×1+0.125×3+0.125×3+0.25×2$$ $$#弹跳次数=1.75$$ 注意是或否问题和公平弹跳之间的联系,问题的预期数量等于弹跳的预期数量。
$$#问题数量=#弹跳次数$$
因此,机器一需要$2$次弹跳来生成一个符号,猜测一个未知符号需要$2$个问题。机器二需要$1.75$次弹跳,我们平均需要问$1.75$个问题。
意味着如果我们需要猜测$100$个符号来自两台机器,我们可以期望问机器一$200$个问题,机器二$175$个问题。这意味着机器二产生的信息较少因为它的输出有更少的**不确定性**或**惊喜**,就是这样。
克劳德·香农称这个平均不确定性的度量为“熵”,他用字母$H$来代表它。香农选择的熵单位基于公平硬币翻转的不确定性,他称之为“比特”,相当于一个公平弹跳。
我们可以用我们的弹跳类比得出相同的结果。熵或H是每个符号的总和,该符号的概率乘以弹跳次数。
$$H=i=1∑npi×#弹跳次数i$$
不同之处在于,我们如何更一般地表达弹跳次数?正如我们所见,弹跳次数取决于我们在树中的深度。我们可以简化这一点,说弹跳次数等于以2为底的对数该级别的结果数。 $$#弹跳次数=log2(# outcomes)$$ 在一个级别的结果数,也基于概率,在该级别的结果数等于该结果的概率的倒数。 $$# outcomes=p1$$
弹跳次数实际上等于以2为底的对数该符号的概率的倒数,这给出我们最终的方程。熵或H,是每个符号的总和,该符号的概率乘以以2为底的对数该符号的概率的倒数。
$$H=i=1∑npi×log2(pi1)$$ 香农以稍有不同的方式写下了这个,只是倒置了对数内的表达式这导致我们添加一个负号,尽管两个公式给出相同的结果。 $$H=−i=1∑npi×log2(pi)$$
让我们总结一下。当所有结果是同样可能性时,熵是最大的。任何时候你远离同样可能的结果,或引入可预测性,熵必须下降。基本思想是,如果信息源的熵下降,这意味着我们可以问更少的问题来猜测结果。多亏了香农,比特,即熵的单位,被采用为我们信息的定量度量,或惊喜的度量。