概率

出处： https://ocw.mit.edu/courses/6-050j-information-and-entropy-spring-2008/pages/probability/ 翻译：ChatGPT

原文版：

【拆分-Chapter5-Probability】 https://www.modevol.com/document/r5jucdi2b4v8do6m421ukqhb

推荐：

【【官方双语】贝叶斯定理，使概率论直觉化】 https://www.bilibili.com/video/BV1R7411a76r/?share_source=copy_web&vd_source=04259c9260832797bf08914e26e438d5

我们一直在考虑一种信息处理系统的模型，其中输入的符号被编码成比特，然后通过“信道”发送到接收器，并解码回符号。见图5.1。


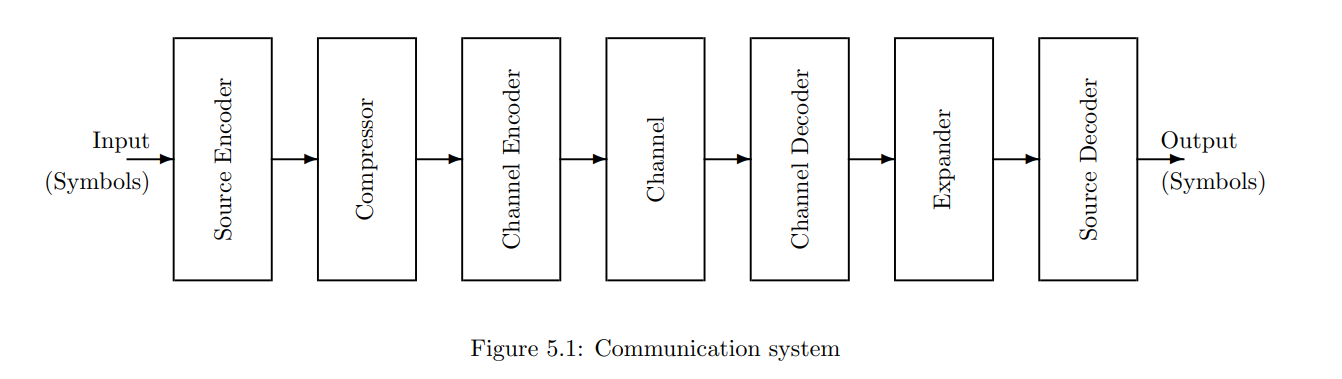
在本笔记的早期章节中，我们已经研究了该模型中的各种组件。现在我们回到信源，并根据概率分布对其进行更全面的建模。

信源提供一个符号或一系列符号，这些符号从某个集合中选择。选择过程可能是一个实验，例如掷硬币或掷骰子。或者，它可能是对未由观察者引起的行为的观察。或者符号序列可能来自某个对象的表示，例如文本中的字符，或图像中的像素。

我们仅考虑有限符号选择的情况，并且仅考虑符号是互斥（一次只能选择一个）且穷尽（实际选择了一个）的情况。每个选择构成一个“结果”，我们的目标是追踪结果的序列及其伴随的信息，从输入到输出。为此，我们需要能够说明结果是什么，以及我们对结果某些属性的了解。

如果我们知道结果，我们有一个非常好的方法来表示结果。我们可以简单地命名所选择的符号，并忽略所有未被选择的符号。但如果我们还不知道结果，或者在某种程度上不确定呢？如果存在不确定性，我们该如何表达我们的知识状态？为此，我们将使用概率数学。

为了说明这个重要的概念，我们将使用基于麻省理工学院学生特征的例子。2007年秋季麻省理工学院的学生官方统计数据^{[^1]}包括表 **5.1** 中的数据，该表以维恩图格式在图 **5.2** 中重现。

1

所有学生的数据可以在以下网址找到： http://web.mit.edu/registrar/www/stats/yreportfinal.html ，所有女性学生的数据可以在以下网址找到： http://web.mit.edu/registrar/www/stats/womenfinal.html



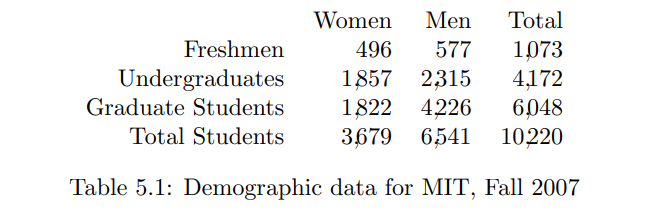
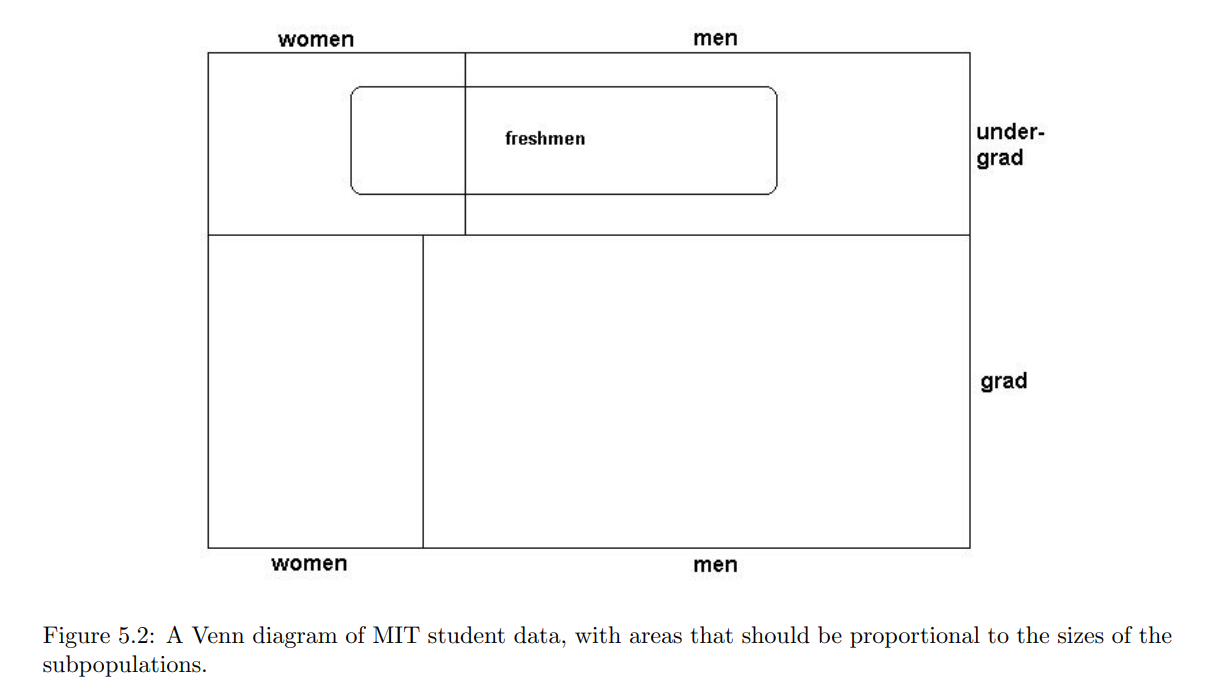
假设选择了一名MIT新生（被选择的符号是个别学生，可能的符号集合是1073名新生），但你没有被告知是谁。你想知道这名学生是女性还是男性。当然，如果你知道所选学生的身份，你就会知道性别。但如果不知道，你如何描述你的认知？选择的是女性的可能性或概率是多少？

注意，2007年新生班级中46%（496/1,073）是女性。这是一个事实，或统计数据，可能代表也可能不代表所选新生是女性的概率。如果你有理由相信所有新生被选择的概率是均等的，你可能会认为被选择的是女性的概率是46%。但是，如果有人告诉你选择是在McCormick Hall（一个女子宿舍）的走廊里进行的，那么所选新生是女性的概率可能会高于46%。统计和概率可以使用相同的数学方法来描述（将在下文中展开），但它们是不同的概念。

5.1 事件

和许多数学或科学分支一样，概率论有其自身的术语，其中一个词的含义可能与其日常含义不同或更具体。考虑两个词：事件（event）和**结果**（outcome）。Merriam-Webster's Collegiate Dictionary 给出了与概率论中的技术含义最接近的定义：

• **结果**：作为结果或后果的某物

• **事件**：实验可能结果的一个子集

在我们的语境中，**结果**是被选择的符号，无论我们是否知道它。虽然谈论尚未进行的选择的结果是错误的，但谈论所考虑选择的可能结果集是可以的。在我们的例子中，这是所有符号的集合。至于**事件**一词，其最常见的日常含义（我们不需要的）是指发生的事情。我们引用的含义列在字典的最后一条。我们将以这种限定的方式使用这个词，因为我们需要一种方法来估计或描述我们对符号各种属性的认知。这些属性是指对每个符号要么适用要么不适用的特性，一种便捷的思考方式是将所有符号的集合分为两个子集，一个具有该属性，另一个不具有。当进行选择时，就会有几个事件。其中一个是结果本身。这称为**基本事件**。其他事件是选择具有特定属性的符号。

尽管严格来说，事件是可能结果的集合，但在概率论中通常将产生这些结果的实验称为事件。因此，我们有时会将选择称为事件。

例如，假设选择了一名MIT新生。所选的具体人是结果。基本事件就是那个人，或选择那个人。另一个事件是选择一个女性（或男性）。另一个事件可能是选择来自加利福尼亚的人，或者年龄超过18岁的人，或身高超过六英尺的人。可以考虑更复杂的事件，例如来自德克萨斯州的女性，或来自密歇根州且有特定SAT成绩的男性。

某个符号被选择的特殊事件必定会发生。我们将这个事件称为**全体事件**，借用了集合论中对应概念的名称。

没有符号被选择的特殊“事件”称为**空事件**。空事件不可能发生，因为只有在进行选择后结果才定义。

不同的事件可能会或可能不会重叠，从某种意义上说，同一个结果可以导致两个或多个事件同时发生。一组不重叠的事件称为**互斥事件**。

例如，选择的新生（1）来自俄亥俄州，或（2）来自加利福尼亚，这两个事件是互斥的。

若干事件可能具有这样的性质，即任何符号被选择时至少有一个事件会发生。一组事件，其中一个确定会发生，称为**穷尽事件**。

例如，选择的新生（1）年龄小于25岁，或（2）年龄大于17岁，这些事件是穷尽的，但不是互斥的。

既互斥又穷尽的一组事件称为**划分**。由所有基本事件组成的划分称为**基本划分**。

在我们的例子中，选择女性和选择男性这两个事件构成了一个划分，而与1073个个人选择中的每一个相关的基本事件构成了基本划分。

由少数事件组成的划分，其中一些事件可能对应于许多符号，称为**粗粒划分**，而包含许多事件的划分称为**细粒划分**。基本划分是最细粒的划分。由全体事件和空事件组成的划分是最粗粒的划分。

尽管我们描述事件时好像总有一个基本划分，但在实际中不必使用这个划分。

5.2 已知结果

一旦你知道了结果，表示它就很简单。你只需指定选择了哪个符号。如果其他事件是基于这些符号定义的，那么你就知道哪些事件已经发生。然而，在结果未知之前，你无法以这种方式表达你的认知。而且，当然要记住，你的知识可能与其他人的知识不同，即知识是主观的，或者说是“观察者依赖的”。

这里有一种表示已知结果的更复杂的方法，这种方法很有用，因为它可以推广到结果尚未知的情况。设 $i$ 为划分中的一个索引。由于符号的数量是有限的，我们可以认为这个索引从 $0$ 到 $n−1$，其中 $n$ 是划分中事件的数量。那么对于划分中的任何特定事件 $Ai​$，定义 $p(Ai​)$ 为 $1$（如果选择了对应的结果）或 $0$（如果未选择）。在任何划分中，恰好有一个 $i$ 使得 $p(Ai​)=1$，而所有其他 $p(Ai​)$ 都为 $0$。这个相同的表示法也适用于不在划分中的事件——如果选择的结果导致事件 $A$ 发生，那么 $p(A)=1$，否则 $p(A)=0$。

根据这个定义，$p(全体事件)=1$ 和 $p(空事件)=0$。

5.3 未知结果

如果符号尚未被选择，或者你尚未知道结果，那么每个 $p(A)$ 可以被赋予一个在 $0$ 和 $1$ 之间的数值，数值越大表示对该事件将发生的信念越强，数值越小表示对该事件可能不会发生的信念越强。如果你确定某个事件 $A$ 不可能发生，那么 $p(A)=0$。如果得知结果，每个 $p(A)$ 可以调整为 $0$ 或 $1$。再次注意，$p(A)$ 取决于你的认知状态，因此是主观的。

这些数值应如何分配以最佳地表达我们的知识将在后面的章节中详细讨论。然而，我们要求它们遵循概率论的基本公理，并将它们称为概率（应用于某个划分的概率集称为概率分布）。根据定义，对于任何事件 $A$，

在我们的例子中，我们可以用选中的新生是女性的概率 $p(W)$ 来描述我们对尚未选中（或尚未知道）的新生性别的理解。

同样，$p(CA)$ 可以表示选中的人来自加利福尼亚的概率。

为了与概率论保持一致，如果某个事件 $A$ 仅在某些互斥的其他事件 $Ai​$ 发生时才会发生（例如因为它们来自同一划分），那么 $p(A)$ 是这些事件的 $p(Ai​)$ 的总和：

其中 $i$ 是相关事件的索引。这意味着对于任何划分，由于 $p(全体事件)=1$，

此处的总和是划分中的所有事件。

5.4 联合事件和条件概率

你可能对所选符号具有两种不同属性的概率感兴趣。例如，选择的新生是来自德克萨斯州的女性的概率是多少？如果我们知道选择的是女性的概率 $p(W)$ 和选择的是来自德克萨斯州的概率 $p(TX)$，能否找到 $p(W,TX)$？

一般来说不能。可能有47%的新生是女性，也可能有5%的新生来自德克萨斯州，但这些事实本身并不能保证有德克萨斯州的女性新生，更不用说有多少了。

然而，如果已知或假设两个事件是独立的（一个事件的概率不依赖于另一个事件是否发生），那么可以找到联合事件（两者都发生）的概率。它是两个事件概率的乘积。

在我们的例子中，如果来自德克萨斯州的新生中女性的百分比已知与所有新生中的女性百分比相同，则

由于两个事件独立的情况并不常见，因此需要一个更一般的联合事件公式。这个公式利用了“条件概率”，即在已知另一个事件发生的情况下一个事件的概率。

在我们的例子中，选择的是女性的新生，假设选中的新生来自德克萨斯州的条件概率表示为 $p(W∣TX)$，其中竖线表示“给定”，分隔了两个事件——右边是条件事件，左边是被条件化的事件。如果两个事件是独立的，则被条件化事件的概率与其正常或“无条件”概率相同。

在条件概率的术语中，联合事件的概率是一个事件的概率乘以在该事件已经发生的情况下另一个事件的概率：

注意，任何一个事件都可以作为条件事件，所以这个联合概率有两个公式。使用这些公式，即使你不关心联合概率，也可以从另一个条件概率计算出一个条件概率。

这个公式称为贝叶斯定理，以18世纪首次阐明它的英国数学家托马斯·贝叶斯命名。我们将频繁使用贝叶斯定理。这个定理具有显著的普遍性。如果两个事件在物理上或逻辑上相关，它是正确的，如果它们不相关，它也是正确的。如果一个事件引起另一个事件，它是正确的，如果不是这种情况，它也是正确的。如果结果已知，它是正确的，如果结果未知，它也是正确的。

因此，所选学生是来自德克萨斯州的女性的概率 $p(W,TX)$ 是选择来自德克萨斯州的学生的概率 $p(TX)$ 乘以在选择的是德克萨斯州人的情况下选择女性的概率 $p(W∣TX)$。它也是选择女性的概率 $p(W)$ 乘以在选择的是女性的情况下选择德克萨斯州人的概率 $p(TX∣W)$。

另一个例子，考虑上表中的学生，并假设从整个学生群体中“随机”选择一个（意味着所有学生被选中的概率相等）。选择的是男性研究生的概率 $p(M,G)$ 是多少？这是一个联合概率，如果我们能找到必要的条件概率，可以使用贝叶斯定理。

在这种情况下，基本划分是选择某个特定学生的 $10,220$ 个基本事件。这些概率的总和是 $1$，假设所有的概率相等，所以每个概率是 $1/10,220$，大约 $0.01%$。

选择的是研究生的概率 $p(G)$ 是与研究生相关的所有 6,048 个基本事件的概率之和，所以 $p(G)=6,048/10,220$。

在选择的是研究生的情况下，选择的是男性的条件概率是多少？我们现在查看研究生群体并选择其中一个。新的基本划分是 $6,048$ 个可能的研究生选择，我们从上表中看到，其中 $4,226$ 是男性。这种新（条件）选择的概率可以如下找到。最初的选择是“随机的”，所以所有学生被选中的概率相等。特别地，所有研究生被选中的概率相等，所以新的概率对于所有 $6,048$ 个都是相同的。由于它们的总和是 $1$，所以每个概率是 $1/6,048$。选择男性的事件与这些新基本事件中的 $4,226$ 个相关，所以条件概率 $p(M∣G)=4,226/6,048$。因此根据贝叶斯定理：

这个问题可以从另一个角度来解决：选择男性的概率是 $p(M)=6,541/10,220$，选择的是男性情况下选择研究生的概率是 $p(G∣M)=4,226/6,541$，所以（当然答案是相同的）

5.5 平均值

假设我们想知道在我们的例子中选中的新生的身高。如果我们知道是谁被选中了，我们可以轻易地查出他或她的身高（假设每个新生的身高在某个数据库中都有记录）。但如果我们还不知道选中的人的身份，我们还能估算身高吗？

一开始，可能会认为因为我们不知道是谁被选中，所以对身高一无所知。但这显然不正确，因为经验表明，绝大多数新生的身高在 $60$ 英寸（$5$ 英尺）到 $78$ 英寸（$6$ 英尺 $6$ 英寸）之间，所以我们可能会觉得安全地估算身高为 70 英寸。至少我们不会估算身高为 $82$ 英寸。

通过概率，我们可以更加精确地计算未知选择情况下的估计身高。而且，当我们知道实际选择并相应地调整概率后，这个计算公式仍然适用。

假设我们有一个划分，其中事件 $Ai​$ 每个都具有某个属性的值，例如身高，记作 $hi​$。那么，这个属性的平均值（也称为期望值）$Hav​$ 可以通过与这些事件相关的概率来计算：

这里的求和是针对划分中的所有事件。

这种公式可以用于求得许多属性的平均值，例如 SAT 成绩、体重、年龄或净财富。对于那些非数值属性（如性别、眼睛颜色、性格或预期学术专业）则不适用。

注意，这个平均值的定义适用于划分中的每个事件都具有该属性（如身高）的情况。这对于新生的身高只有在基本划分的情况下才成立。我们希望有类似的方法来计算其他划分的平均值，例如男性和女性的划分。问题是，并非所有男性的身高都相同，因此不清楚在公式 **5.9** 中该使用什么作为 $hi​$。

解决方法是根据更细粒度的划分（如基本划分）来定义男性的平均身高。贝叶斯定理在这方面很有用。注意，假设已知选择的结果是男性，则选中新生 $i$ 的概率为

其中 $p(M∣Ai​)$ 特别简单——它要么是 $1$ 要么是 $0$，取决于新生 $i$ 是男性还是女性。那么，男性新生的平均身高为

同样地，女性的平均身高为

然后，所有新生的平均身高的公式与公式 **5.9** 完全相同：

如果划分中所有 $p(Ai​)$ 都相等（例如，如果新生是“随机”选择的），这些平均值的公式都是有效的。但它们更为普遍——它们也适用于任何概率分布 $p(Ai​)$。

唯一需要注意的是事件的概率为零的情况，例如，如果你想要计算来自内华达州的新生的平均身高，而恰好没有来自内华达州的新生。

5.6 信息

我们希望定量地表达我们对选择符号的了解或缺失信息。在得知结果后，我们对所选符号及其各种属性以及由于选择而可能发生的事件没有任何不确定性。然而，在选择之前或至少在我们知道结果之前，我们存在一定的不确定性。这种不确定性有多大？

在得知结果后，我们现在拥有的信息可以通过指定所选符号来告诉别人。如果有两个可能的符号（例如抛硬币的正反面），那么可以使用一个比特来表示这个结果。如果有四个可能的事件（例如从一副牌中抽取的花色），则可以用两个比特来表示结果。更一般地，如果有 $n$ 个可能的结果，那么需要 $log2​n$ 个比特。

这里的概念是，听到结果后我们所获得的信息量是可以用来告诉我们的最小比特数，即，指定符号的比特数。这种方法有一定的价值，但有两个缺陷。

首先，通过一系列比特实际指定一个符号需要整数个比特。如果符号的数量不是二的整数次幂怎么办？对于单个选择，可能没有太多办法，但如果信源进行重复选择并且这些选择都需要指定，它们可以组合在一起以恢复小数比特。

例如，如果有五个可能的符号，那么单个符号需要三个比特，但两个符号的 $25$ 种可能组合可以用五个比特（每个符号 $2.5$ 比特）来传达，而三个符号的 $125$ 种组合可以用七个比特（每个符号 $2.33$ 比特）来传达。这比 $log2​(5)$（即 $2.32$ 比特）大不了多少。

其次，不同事件被选中的可能性可能不同。我们已经看到如何用概率来建模我们的知识状态。如果我们已经知道结果（某个 $p(Ai​)$ 等于 1，其他所有都等于 0），那么不会获得更多信息，因为之前没有不确定性。我们对信息的定义应涵盖这种情况。

考虑一个有 $32$ 名学生的班级，其中两名是女性，$30$ 名是男性。如果选中一个学生，我们的目标是知道选中了哪一个，我们最初的不确定性是五个比特，因为这是指定结果所需的比特数。如果随机选中一个学生，每个学生被选中的概率是 $1/32$。选择学生也会导致一个性别事件，即“选择了女性”，概率 $p(W)=2/32$，或“选择了男性”，概率 $p(M)=30/32$。

如果我们被告知选中的人是女性但不知道具体是谁，我们获得了多少信息？我们的不确定性从五个比特减少到一个比特（指定是哪两个女性之一所需的比特数）。因此，我们获得了四个比特的信息。如果我们被告知选中的人是男性但不知道具体是谁，我们的不确定性从五个比特减少到 $log2​(30)$ 或 $4.91$ 比特。因此，我们获得了 $0.09$ 比特的信息。

这里的重点是，如果我们有一个事件具有不同概率的划分，从不同结果中获得的信息量不同。如果结果是可能的，我们学到的信息比结果是不太可能的情况少。我们在一个案例中说明了这一原则，其中每个结果都未解决从基本划分中选择一个事件的问题，但该原则即使在我们不关心基本划分的情况下也适用。从结果 $i$ 中获得的信息量是 $log2​(1/p(Ai​))$。从这个公式可以看出，如果某个 $i$ 的 $p(Ai​)=1$，则从该结果中获得的信息量为 $0$，因为 $log2​(1)=0$。这与我们的预期一致。

如果我们想在得知结果之前量化我们的不确定性，我们不能使用特定结果所获得的任何信息，因为我们不知道使用哪个。相反，我们必须对所有可能的结果进行平均，即，对具有非零概率的划分中的所有事件进行平均。每个事件的平均信息量通过将每个事件 $Ai​$ 的信息乘以 $p(Ai​)$ 并对划分求和得到：

这个量对描述信源的信息具有根本重要性，称为信源的**熵**。这个公式在所有概率相等时有效，在概率不相等时也有效；在结果已知且概率调整使其中一个为 $1$ 而其他所有为 $0$ 时有效；无论所报告的事件是否来自基本划分，该公式都有效。

在信息的这些公式中，必须注意具有零概率的事件。这些情况可以处理为具有非常小但非零概率。在这种情况下，尽管对趋近于无穷大的参数，日志趋近于无穷大，但它的趋近速度非常慢。该因子乘以概率的乘积趋近于零，因此这些项可以直接设为零，即使公式可能表明不确定结果，或者计算程序可能出现“除以零”错误。

5.7 信息的性质

将物理量视为具有维度是很方便的。例如，速度的维度是长度除以时间，因此速度以米每秒表示。同样，将信息视为具有维度的物理量也是方便的。也许这不那么自然，因为概率本质上是无维的。然而，请注意公式使用了以 $2$ 为底的对数。底的选择相当于信息的比例因子。原则上，任何底 $k$ 都可以使用，并通过以下等式与我们的定义相关联：

使用底为 $2$ 的对数时，信息以比特表示。稍后，我们会发现自然对数也很有用。

如果划分中有两个事件，概率分别为 $p$ 和 $1−p$，每个符号的信息量为

如图 **5.3** 所示，这是 $p$ 的函数。对于 $p=0.5$，信息量最大（1 比特）。因此，当两个可能事件的概率相等时，信息量达到最大。此外，对于 $p=0.4$ 和 $p=0.6$ 之间的概率范围，信息量接近 1 比特。对于 $p=0$ 和 $p=1$ 时，信息量等于 0。这是合理的，因为对于这样的 $p$ 值，结果是确定的，因此学习它不会获得任何信息。


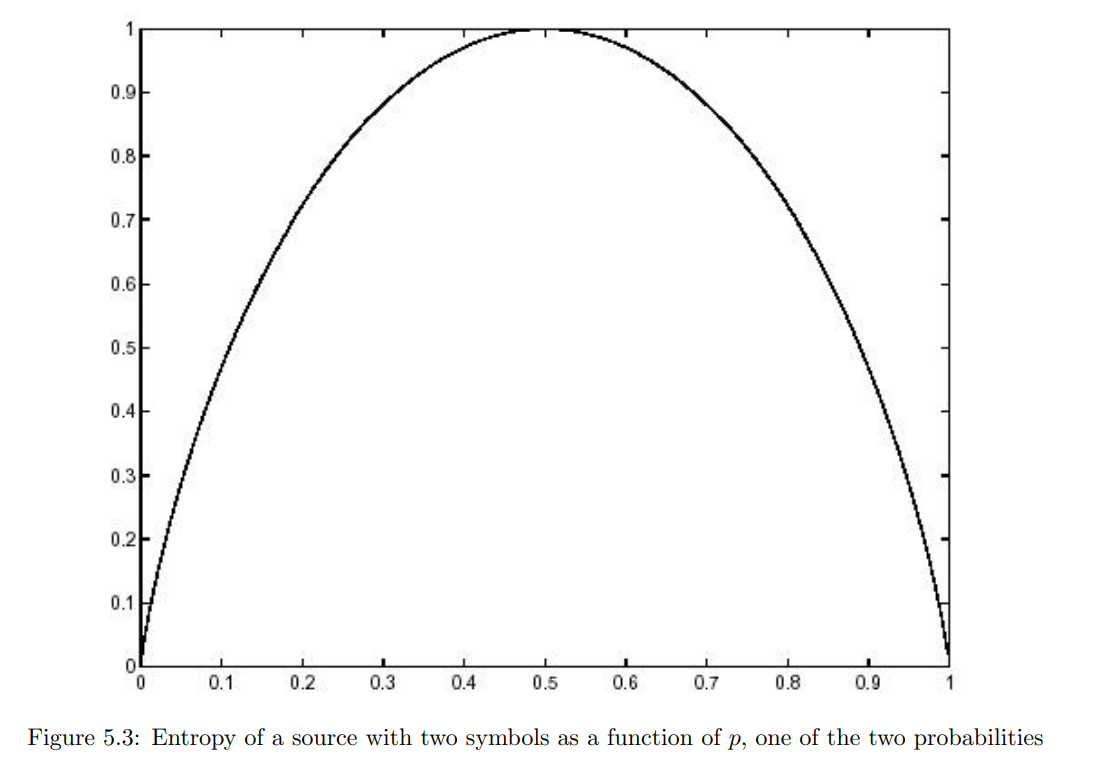
对于有多个可能事件的划分，每个符号的信息量可以更高。如果有 $n$ 个可能的事件，每个符号的信息量介于 $0$ 和 $log2​(n)$ 比特之间，当所有概率相等时，达到最大值。

5.8 高效信源编码

如果一个信源有 $n$ 个可能的符号，那么一个固定长度的编码将需要每个符号 $log2​(n)$（或更高的整数）比特。每个符号的平均信息量 $I$ 不能超过这个值，但如果符号具有不同的概率，$I$ 可能会更小。是否可以通过使用可变长度编码为更可能的符号使用更少的比特，为不太可能的符号使用更多的比特，从而在平均情况下用更少的比特来编码一串符号？

当然可以。莫尔斯电码是一个可变长度编码的例子，能够很好地实现这一点。

存在一种通用的构造这种高效编码的方法，这些编码非常高效（实际上，即使 $I$ 远低于 $log2​(n)$，它们每个符号所需的平均比特数也小于 $I+1$）。这些编码称为哈夫曼编码，以 MIT 毕业生大卫·哈夫曼（1925-1999）的名字命名，它们广泛应用于通信系统中。见第 **5.10** 节。

5.9 细节：人寿保险

一个统计和概率在日常生活中的例子是它们在人寿保险中的应用。我们这里只考虑一年期定期保险（保险公司在市场上非常有创意地推出了更复杂的保单，这些保单结合了保险、储蓄、投资、退休收入和税收最小化等方面）。

当你购买一份人寿保险时，你支付一定金额的保费，如果你在这一年内去世，你的受益人将获得一笔更大的金额。人寿保险可以从多种角度进行思考。

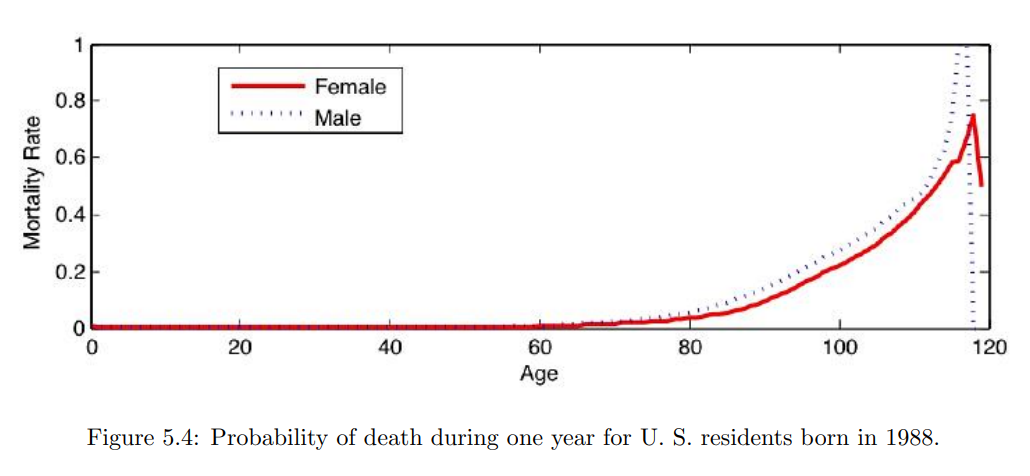
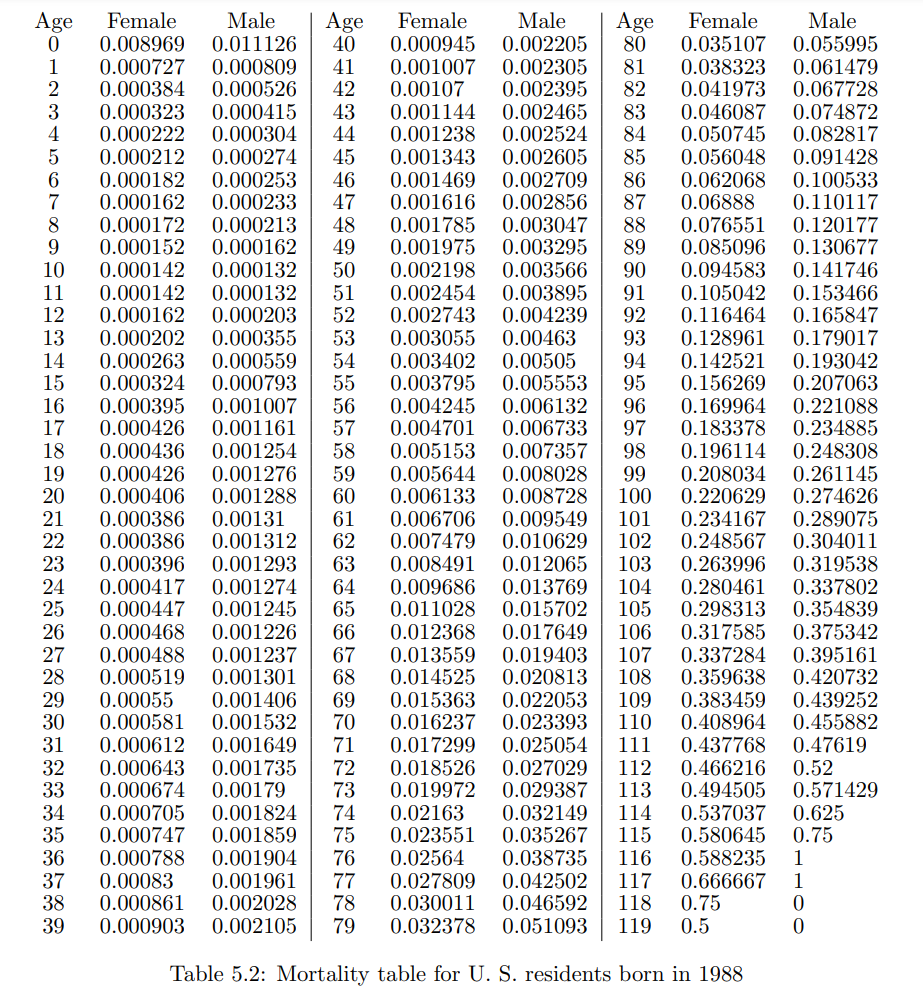
从赌徒的角度来看，你在赌自己会死，保险公司在赌你会活。你们每个人都可以估计你死亡的概率，由于概率是主观的，它们可能存在足够的差异，使得这种赌注对双方都显得有利（例如，假设你知道一个威胁性的健康状况，但没有向保险公司披露）。保险公司使用如表 **5.2**（在图 **5.4** 中也显示）的死亡率表来设定费率。（有趣的是，保险公司也出售年金，从赌徒的角度来看，这些年金是相反的赌注——公司在赌你很快会死，而你在赌自己会活很长时间。）



另一种思考人寿保险的方法是将其视为一种金融投资。由于保险公司平均支付的金额少于他们收取的金额（否则他们会破产），投资者通常会通过其他方式投资他们的钱获得更好的收益，例如把钱存入银行。

当然，大多数购买人寿保险的人不将其视为赌注或投资，而是将其视为一种安全网。他们知道，如果自己去世，他们的收入将停止，他们希望为他们的受养人，通常是孩子和配偶，提供部分替代。这笔保费很小，因为在这种安全网重要的年份里死亡的概率很低，但在死亡不太可能发生的情况下，这种福利对受益人可能非常重要。对于非常富有的人（能够承受收入损失），没有受养人的单身人士，或者子女已经长大的老年人来说，这种安全网可能并不那么重要。

图 **5.4** 和表 **5.2** 显示了1988年出生的美国居民在一年内死亡的概率，作为年龄的函数（数据来自伯克利死亡率数据库^{[^2]}）。

2

伯克利死亡率数据库可以在线访问： http://www.demog.berkeley.edu/bmd/states.html

5.10 细节：高效信源编码

有时，通信系统中的信源编码和压缩（如图 **5.1** 所示）是一起完成的（是否将信源和信道编码结合起来有实际的好处仍然是一个开放的问题）。对于具有有限数量符号但输入流中出现概率不均的信源，有一种优雅而简单的信源编码技术，具有最小冗余。

有限信源的示例

考虑一个生成 MIT 成绩符号的信源，可能的值是 A、B、C、D 和 F。要求你设计一个系统，该系统可以以每秒一个符号的速度通过只能每秒传输两个布尔位（每个 $0$ 或 $1$）的通信信道传输这些成绩流^{[^3]}。

3

布尔位或二进制位通常称为“比特”。“比特”这个词也指信息的单位。当一个布尔位携带确切的一比特信息时，可能没有混淆。但是效率低下的编码或冗余编码可能具有长于最小值的布尔位序列，因此每个比特携带少于一比特的信息。这种混淆也存在于其他度量单位，例如米、秒等。

首先，假设对成绩分布没有任何了解。要分别传输每个符号，你必须将每个符号编码为比特序列（布尔位）。使用 $7$ 位 ASCII 编码是浪费的；我们只有五个符号，而 ASCII 可以处理 $128$ 个。由于只有五个可能的值，成绩可以用每个符号三比特编码。但是信道每秒只能处理两个比特。

然而，三比特是多余的。假设对概率没有任何信息，熵最多为 $log2​(5)=2.32$ 比特。这也是 $i∑​p(Ai​)log2​(1/p(Ai​))$，其中有五个 $pi​$，每个等于 $1/5$。为什么我们在第一种情况下需要三比特？因为我们没有办法传输部分比特。为了做得更好，我们可以使用“块编码”。我们将符号分组成例如三个一组。每个块的信息是每个符号的信息的三倍，即 $6.97$ 比特。因此，一个块可以使用 $7$ 个布尔比特传输（有 $125$ 个不同的三个成绩的序列，$7$ 个比特有 $128$ 种可能的模式）。当然，我们还需要一种方式表示结束，并且一种方式表示最后传输的词只有一个有效的成绩（或两个），而不是三个。

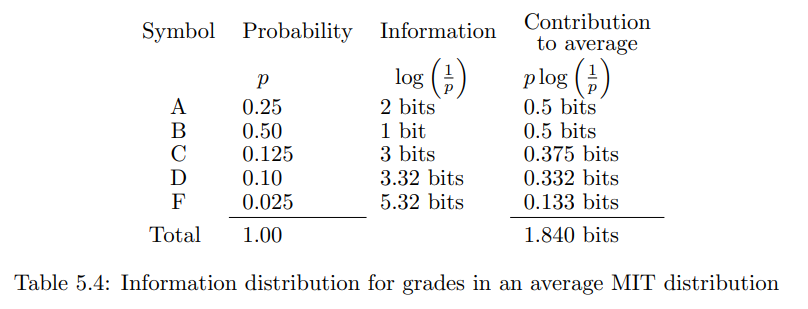
但这仍然是信道处理能力太多的比特。因此，让我们看看符号的概率分布。在一个典型的“以 B 为中心”的 MIT 课程中，成绩分布可能如表 $5.3$ 所示。假设这是一个概率分布，每个符号的信息量和平均每个符号的信息量是多少？此计算在表 $5.4$ 中显示。每个符号的信息量为 $1.840$ 比特。由于这小于两个比特，可能可以对符号进行编码以使用该信道。



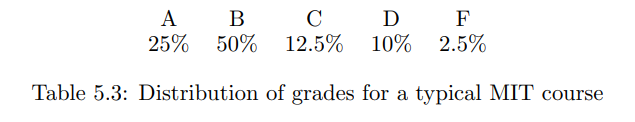
哈夫曼编码

大卫·A·哈夫曼（David A. Huffman，1925年8月9日-1999年10月6日）是麻省理工学院的一名研究生。在他从罗伯特·M·法诺教授（Prof. Robert M. Fano）那里修读的一门课程的作业中，他设计了一种编码方法，能够以最小冗余和不需要特殊符号帧的方式编码具有不同概率的符号，从而实现最紧凑的编码。他在1962年9月的《IRE会议录》（Proceedings of the IRE）中描述了这一算法。这个算法非常简单。其目标是提出一本“代码书”（每个符号对应一个比特串），使平均代码长度最小。假设不常见的符号将获得较长的代码，而常见的符号则获得较短的代码，就像莫尔斯电码一样。算法如下（可以参考表 $5.5$）：

1. **初始化**：最初每个符号的部分代码为空比特串。为每个符号定义一个“符号集”，其中仅包含该符号，概率等于该符号的概率。

2. **循环测试**：如果只有一个符号集（其概率必须是1），则完成。代码书由该符号集中每个符号对应的代码组成。

3. **循环操作**：如果有两个或更多符号集，则选择概率最低的两个符号集（如果有相同概率，则任选两个）。将其中一个符号集的代码前面加上0，另一个符号集的代码前面加上1。定义一个新的符号集，它是刚处理的两个符号集的并集，概率等于这两个概率的和。用新的符号集替换这两个符号集，符号集的数量减少一个。重复这个循环，包括循环测试，直到只剩下一个符号集。

请注意，这个过程通常会产生可变长度的代码。如果有 $n$ 个不同的符号，至少有两个符号的代码长度是最长的。

在我们的例子中，我们从五个符号集开始，每步将符号集的数量减少一个，直到只剩下一个符号集。步骤如表 **5.5** 所示，最终的代码书如表 **5.6** 所示。



确实，这种编码非常紧凑。最频繁的符号（B）被赋予了最短的代码，而最不频繁的符号（D 和 F）则得到了最长的代码，因此对于符合假设概率分布的输入流，所需的平均比特数确实很短，如表 5.7 所示。


将此表与之前的信息内容表（表 5.4）进行比较。注意，每个符号的平均编码长度为 1.875 比特，而每个符号的信息量为 1.840 比特。这是因为符号 D 和 F 不能以小数比特编码。如果将几个符号的块一起考虑，哈夫曼编码的平均长度可能会更接近实际的每符号信息量，但不会低于它。

该信道每秒可以处理两个比特。通过使用这种编码，你可以平均每秒通过信道传输稍多于一个符号。你可以实现你的设计目标。

关于哈夫曼编码，有至少六个实际问题需要考虑：

• 可能会出现一连串的 D 或 F 成绩。编码器需要存储这些比特，直到信道能够赶上。需要多大的缓冲区来存储？如果缓冲区溢出会发生什么？

• 由于缓冲备份，输出可能会延迟。输入与相关输出之间的时间称为“延迟”。对于交互式系统，你希望保持低延迟。每秒处理的比特数，即“吞吐量”，在非交互式应用中更为重要。

• 由于突发导致的延迟，输出不会在定期间隔发生。在某些实时应用（如音频）中，这可能很重要。

• 如果我们假定的概率分布是错误的会怎样？一个大型课程可能会给出较少的 A 和 B 成绩，而更多的 C 和 D 成绩。我们的编码将效率低下，可能会导致缓冲区溢出。

• 解码器需要知道如何将比特流分解成单个代码。在这种情况下的规则是，遇到'1'或'0000'时中断。然而，有许多可能的哈夫曼代码，对应于步骤3中对0和1的不同选择。大多数没有如此简单的规则。虽然总是可以做到，但很难知道应该将符号间断放在哪里。

• 编码表本身必须提前提供给编码器和解码器。这可以通过一次在信道上传输编码表来完成。

另一个例子

MIT 的新生在第一学期使用“通过/无记录”系统。成绩 A、B 和 C 在成绩单上显示为 P（通过），而 D 和 F 不显示（在我们的示例中，我们将其指定为无记录，N）。让我们设计一个系统，以最快的平均速率将这些 P 和 N 符号发送到打印机。如果不考虑概率，每个符号需要 $1$ 比特。但概率（假设表 **5.3** 中典型的 MIT 成绩分布）为 $p(P)=p(A)+p(B)+p(C)=0.875$，$p(N)=p(D)+p(F)=0.125$。因此，每个符号的信息量不是 $1$ 比特，而是 $0.875×log2​(1/0.875)+0.125×log2​(1/0.125)=0.544$ 比特。对单个符号进行哈夫曼编码没有帮助。我们需要将比特组合在一起。例如，十一种成绩作为一个块有 $5.98$ 比特的信息，可以原则上编码为仅需 $6$ 比特发送到打印机。

MIT 开放课程资源
[http://ocw.mit.edu](http://ocw.mit.edu/)

6.050J / 2.110J 信息与熵
2008 春季

关于引用这些资料或我们的使用条款的信息，请访问： [http://ocw.mit.edu/terms](http://ocw.mit.edu/terms)。