#前言
本文为联合发布,语言学概念部分由@还休提供。数学概念部分由@郭慧提供,信息学部分由@心雨之林和@思无邪提供。 欢迎各位食用,并提出建议。 #语言学概念 ##0. 概念 ###0.1概念
当我们在说你要明确概念的时候,我们在说什么?
“概念”是通过抽象化的方式从一群事物中提取的能够反映其共同特征的最基本的知识单元,又是我们思考的最小的知识单元,同时也是客观事物在人脑中的反映。
比如说,人是一个概念。人是有语言,能思维,会制造工具的高等动物,其中“有语言,能思维,会制造工具的高等动物”就是通过抽象提取出来的共性。
三角形也是一个概念。三角形是把一群图形抽象出三角三边的共性,所形成的一类事物。例如,最常见的三角板,埃及的金字塔平面形状,我们夏天吃的竹笋的平面外形。
###0.2 基本组成 ####0.2.1 内涵
每一个概念都有它的含义,比如说“人”这个概念的含义就是指“有语言,能思维,会制造工具的高等动物”。概念的含义叫做概念的内涵。它表示概念所反映的事物的共性。
那么,人的内涵就是有语言,能思维,会制造工具。
例如,数学中常见的集合,一个集合的内涵指的是这个集合的共性。现在有这样一个集合{2,4,6,8},那么,正数、偶数都是集合这个概念的内涵。
再比如三角形的内涵指是三角形的共性,那么三个角,三条边、内角和180°,这些都是三角形这个概念的内涵 ####0.2.2 外延
每一个概念都有它的适用范围,比如说“人”这个概念的适用范围就包括“活着的人,死去的人,中国人,外国人”,但不适用与猫,狗等。这种概念所适用的范围叫做概念的外延。
例如,集合这个概念的外延是指集合所适用的范围,也是指集合内的所有元素。假设当前有一个集合是{2,4,6,8},那么集合内所有元素2,4,6,8就是这个集合的外延。
同理,三角形这个概念的外延指的是三角形所适用的范围,也就是指所有类型的三角形,比如说:等腰三角形,等边三角形,直角三角形,锐角三角形,钝角三角形等。 ####0.2.3 外延与内涵关系
概念的内涵和外延是一对矛盾,共处于统一体的概念之中,它们之间是相处依存,相互制约的关系。一个概念的内涵扩大,它的外延就缩小;一个概念的内涵缩小,则外延扩大。
例如当前这个集合{2,4,6,8}中若是增加“都是合数”这一共性,则“2”就被pass掉了,集合只剩下{4,6,8},此时集合的适用范围缩小。
再比如,三角形的内涵若是增加“相邻两边相等”这一共性,你会发现直角三角形就被pass掉了,外延缩小。若是再增加“三条边都相等”这一共性,则此时三角形这个概念只剩下等边三角形,外延进一步缩小。
##1. 命题 ###1.1 命题
现在我们知道了什么是概念,而生活中往往遇到让我们困惑的是不仅仅是概念,更多的是概念与概念之间的关系。
这种表达概念与概念之间关系的叫做命题。在数学中,命题也是表达真或假的陈述。
比如说:“人都会死”是一个命题。这个命题由“人”和“死亡”这两个概念构成,这个命题就是这两个概念之间的关系。
再比如说:“人会永生”也是一个命题。这个命题由“人”和“永生”这两个概念构成,这个命题就是这两个概念之间的关系
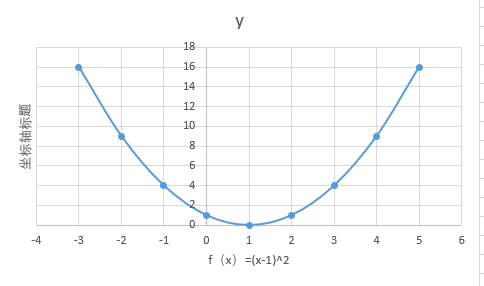
比如说这样一个数学命题:“若x>1,则f(x)=(x−1)2在区间内单调递增”。这里就涉及到“x”、“f(x)=(x-1)^2”、“区间”和“单调递增”这几个概念,该命题则是表达出这几个概念之间的关系。
此处,我们可以看到上面两个命题“人都会死”和“人会永生”,这两个命题是相对立,但根据我们的知识可知,“人都会死”这个命题是正确的,反之,“人会永生”这个命题是错误的。于是,我们得出命题的特点,即命题非真即假。
###1.2 真假命题
于是正确的命题叫做真命题。
所以,人都会死这个命题是真命题。
再比如上述的数学命题:“若x>1,则f(x)=(x−1)2在区间内单调递增”。我们通过作图可知,“当x>1时,该函数在区间内为单调递增”该命题为正确,所以该命题是真命题。
错误的命题叫做假命题。
所以,人会永生这个命题是假命题。
同样,若数学命题:“若x>1,则f(x)=(x−1)2在区间内单调递减”。通过上图我们可知,该命题是错误的,所以是假命题。
##2. 表征 ###2.1 表征
现在我们知道了概念和命题,也能对生活中很多信息加以甄别。那么,你是否有疑问,我们的大脑是如何甄别这些信息,这些信息在我们大脑中的呈现方式是什么?这样的呈现方式我们称为表征。
表征又称再现,是信息在头脑中的呈现方式,是信息记载或表达的方式。表征的核心是一个“替代品”。
比如说,我们从糖中抽象出一个概念“有色带有甜味的晶状体”,这个概念是你给糖所选择的一个替代,并不是真正的糖,所以“有色带有甜味的晶状体”在这里叫做糖的一个表征。这个表征就是糖这种东西在你脑中的呈现方式。
又或者说,有些人认为糖只包含白糖,他们给糖的表征就是“白色带有甜味的晶状体”,在他们眼里,所有的糖都会被“白色带有甜味的晶状体”替代。
#数学概念 ##1.常量
广义概念是指,不变化的量。数学上也称常数,是一种恒定的或不可变的数值或数据项。
在计算机程序运行时,不会被程序修改的量。
三角形的面积公式:S=ah/2;若到了具体的三角形中,给定了底a=3,高h=4;那么这个具体的底和高的值就是常量。
“苏格拉底会死”,这里的“苏格拉底”是一个具体的人,是常量。
##2.变量
广义概念上,跟常量相对,是变化的量。数学上是指没有固定的值,是可以改变的数。
所有人都会死。这里的“所有人”是指“每个人”,没有固定成哪一个人,就是变量。
物体呈直线运动。这里的“物体”没有固定成某一物体,没有具体的物体指向,就是变量。
三角形的面积公式:S=ah/2;底a和高h没有指向到某个具体三角形的底和高,均是变量。
##2.5 自变量VS因变量
任何一个系统(或模型)都是由各种变量构成的,当我们分析这些系统(或模型)时,可以选择研究其中一些变量对另一些变量的影响,那么我们选择的这些变量就称为自变量,而被影响的量就被称为因变量。
函数y=f(x)中,x、y均为变量,X能够影响y的变化,x是自变量,y是因变量。
西瓜两块钱一斤,买3斤西瓜需要6块钱,买5斤西瓜需要10块钱。西瓜总价随着所购买西瓜重量的变化而变化,那么西瓜的重量就是“自变量”,西瓜总价就是“因变量”。
##3.集合
集合是由一个或多个确定的元素所构成的整体。
全中国人的集合,它是指所有的中国人组成的整体,它的元素就是每一个中国人。
光学中的三原色,红、绿、蓝,可以组成一个集合。
英语字母表,是由26个英语字母所组成的一个集合。
##4.映射
映射是两个集合之间元素的对应关系。
设A={1,2,3,4},B={3,5,7,9},集合A中的元素x按照对应关系“乘2加1”和集合B中的元素对应,这个对应是集合A到集合B的映射。
设A=N(N为自然数),B={0,1},集合A中的元素按照对应关系“x除以2得的余数”和集合B中的元素对应,这个对应是集合A到集合B的映射。
衣服的单价为10块钱一件,买3件衣服需要30块钱,买5件衣服需要50块钱。那么衣服的件数按照对应关系“单价X件数=总价”和衣服的总价对应,这个对应就是件数到总价的映射。
##5.空间
空间是一类特殊的集合,而且是一个能够容纳所有你要描述内容的集合。
所有整数的集合加上加法运算,就可看做是一个空间。
带有加法和标量乘法的集合,称为向量空间。
我们将随机试验E的一切可能基本结果组成的集合称为E的样本空间。
“所有人都会死”,输入为:{任意人},输出为:{生死},这里是输入输出是变量;输入空间为{所有人},输出空间为{会死,不会死}。这里的输入/输出空间强调变量引起了变化的范围,即:任意人(变量) 变化范围是 {所有人},生死(变量)变化范围是{会死,不会死}
##6.维度
维度是可以独立变化的因素的个数。
espresso意式浓缩咖啡的做法,多少咖啡粉要冲多少咖啡液,情况是无限的。后来老外不断尝试,找到了一个比例,咖啡粉:咖啡液 = 1 : 2.3;咖啡粉是输入x,咖啡液是输出y,这时就可以利用 y = 2.3x 这个模型来预测所有的情况。 这里的输入仅考虑了一个因素“咖啡粉”,那么我们可以说模型的输入仅考虑了一个维度。 当加入另一个变量“温度”时,模型中的输入就有两个独立变化的因素(“咖啡粉”、“温度”),那么我们可以说模型的输入考虑了两个维度。 再加入第三个变量“研磨度”时,模型中的输入就有了三个独立变化的因素(“咖啡粉”、“温度”、“研磨度”),那么我们可以说模型的输入考虑了三个维度。
英语听力所涉及的输入因素很多,比如音调的高低、口音的不同、发声的长短等,这些都是可以独立变化的因素,那么我们就可以说英语听力所涉及的输入维度很高。 信息学概念
#信息学基本概念 ##1.事件与不确定性
当一件事情只有一种情况发生的时候,这样的事件称之为确定性事件。
例如「太阳升起」这个事件,它只有一种情况,便是「从东边升起」,它既不会从西边,也不会从南边、从北边、从其他任何方向升起,因此,「太阳升起」这个事件称之为确定性事件。
但现实生活中,类似于「太阳升起」这样只有一种情况的事件较少,大多数情况,一个事件对应着很多种可能的情况。
当一个事件存在多种情况发生,而每一次发生不知道是这些情况中的哪一种时,这样的事件称之为不确定性事件。正是由于不确定事件的存在,我们人类才无法做到全知全能,通晓万物,也正是如此,人类才有想要去消解这些不确定性事件的想法,从而产生了「信息学」这门学科。
比较常见的一种不确定性事件便是「一个学生的考试分数」,严格来说,满分100分的卷子,一个学生拿这套卷子考试所得的分数,在区间{0-100}都有可能,(不考虑小数情况下)有101种可能的情况发生,于是「一个学生的考试分数」这个事件称之为不确定性事件。
##2.不确定性的度量
当一个事件有两种情况时(例如抛硬币),我们可能会说这个事件的不确定性较小;当一个事件有101种情况时(例如考试分数),我们可能会说这个事件的不确定性较大。那么我们是通过什么来判断一个事件的不确定性程度呢?
首先我们给这样的不确定性命名为熵,即当一个事件有多种可能情况时,这个事件对某人而言具体是哪种情况的不确定性叫做熵。
不要觉得熵是一个很“高大上”的概念。你可以想象一下这样一种情况,你遇到一个陌生人,他高个子、留着胡须......你之后会多次提及这个人,但你总不能每次提到他,都用一连串的“他高个子、留着胡须”来指代他,于是你用了一个人名“张飞”专门指代这个人,以后每次提他的时候就不用那么费劲了。而“熵”正是这样一个词,当你以它命名,之后每次提到「一个事件的不确定性」,你就可以用「熵」来指代了。
接下来,就像用「年龄」来形容一个人有多老(年轻)一样,我们会说这个人多少岁,这里的「岁」便是「年龄」的基本单位。那么我们用什么来说明熵的大小呢?
我们用bit(比特)作为熵的基本单位。对比而言,1比特我们说熵比较小,而10比特我们说熵比较大。
这是一个全新的概念,因为bit不是我们所说的比特币,但比特币的先入为主的概念会影响我们对于这个基本单位的理解,于是我们应该心生疑问,这个比特是怎么规定出来的?
我们拿生活中常见的概念来类比:千克是质量的基本单位,如果我们要判断一个东西质量是多少,首先得知道1千克是多少。于是我们人为规定(注意是“人为”)一块石头的质量是1千克,那么一头大象的质量有多重,就看它相当于多少块这样的石头,这就是质量度量的逻辑。
按照这个逻辑,我们就应该规定一个基本单位,那就是什么样的事件的熵是1比特,聪明的你马上想到,最简单的事件不就是抛硬币嘛。抛硬币这样的事件有两种可能性(正面和反面),我们就人为规定它的熵为1比特。
有了对于1比特的规定之后,我们碰到其他事件,就拿它与抛硬币做对比,以此算出它的熵的大小。前面我们类比了质量,一头大象的质量相当于多少块1千克的石头,采用的是数学中乘法/除法的方式,但在对熵的度量中,方式则有所不同。 我们规定1比特是抛一次硬币这个事件的熵的大小,它有两种情况。如果一个事件有四种情况,那么它是抛几次硬币对应的结果呢?我们知道抛两次硬币对应正正、正反、反正、反反四种情况,于是如果一个事件有四种情况,那么它是抛两次硬币对应的结果,因而这个事件熵的大小便是2比特。而这用到的就不是数学中乘法/除法的方式,而是幂/对数的方式了,即:
22=4 log24=2
上述过程隐含了一个大前提:我们抛掷硬币的两种情况——正面与反面,它们发生的概率是相同的,即都是50%,而不是正面10%、反面90%。同样,当我们说一个事件有四种情况的时候,它的熵的大小是2比特,也有这样一个前提条件,即:这四种情况是等概率的(均为25%)。
那么聪明的你会问,正如你所说,如果有一个事件,它有两种情况,而且正好一种情况发生的概率是10%,另一种情况发生的概率是90%,这个事件的熵是多少呢?
不等概率熵的度量稍微难以理解,但仍需要你充满耐心。我们认为一个基本的逻辑便是,上述这样的事件熵的大小等于每一种情况发生的概率乘以每一种情况的熵的大小,然后再求和。如果用A来表示事件,a1表示第一种情况,a2表示第二种情况,S( )表示事件的熵,则公式如下:
S(A)=0.1∗S(a1)+0.9∗S(a2)
现在需要解决的问题便是,如何计算概率为10%和90%的熵是多少?即S(a1)和S(a2)的大小? 我们需要做一下转化,即认为10%概率的事件,相当于10种等概率情况中发生其中任意一种,于是它的熵的大小按照等概率计算公式,便能得到:
S(a1)=log210=log21/0.1
可以看到概率的倒数,变成了等概率情况的个数,将其转化为等概率情况的个数之后,就回到了我们熟悉的领域,便可得到其熵的大小。 由此,我们便能得到概率为90%的事件的熵的大小:
S(a2)=log21/0.9=log210/9
汇总起来,我们便回答了这个问题:
S(A)=0.1∗log21/0.1+0.9∗log21/0.9
这便是事件存在多种不等概率情况下,其熵的计算方法。
当然我们上述的一般公式,也需得满足等概率情况(等概率是特殊的一种不等概率),否则就无法形成逻辑的闭环,于是我们可以自行证明一下,1比特的抛硬币事件,正面概率50%,反面概率是50%,如果用不等概率公式计算,它究竟是不是1比特呢?验证如下:
S(A)=0.5∗log21/0.5+0.5∗log21/0.5=0.5∗log22+0.5∗log22=0.5+0.5=1
##3.消除不确定性
既然我们碰到了不确定事件,而且通过上述介绍,我们也知道它的熵是多少了,那么我们如何消除这种不确定性呢?它又需要什么东西来满足呢?
于是,一个广为人知的概念便应运而生,大多数人知道「信息」这个概念,但可能不太了解它表达的究竟是什么?它有什么用?
学习了上述关于不确定性和熵的概念之后,我们便可知道:能够消除某人对一件事情不确定性的事物便是信息。
信息的基本单位也是比特,更重要的是信息与熵是两个此消彼长的概念。当某人对一个事件没有任何信息的时候,该事件的熵对于该人来说是最大的;随着某人不断地获取信息,该事件的熵对于他来说逐渐减少;直至该人获得了该事件的全部信息,该事件便从不确定转变成完全确定,这个时候该事件的熵对于该人来说就是0了。
这很像一个小孩从另外一个小孩篮子里抢苹果。最初甲小孩篮子里苹果最多,乙小孩苹果最少。获取信息的过程,就像乙小孩不断从甲小孩篮子里抢苹果,放到自己篮子里一样,直至把甲小孩篮子里的苹果拿光。
为了让大家更清楚地明白信息与熵的关系,我们来看一个学生最常见的事情之一——做选择题,透过这个例子,你将明白“此消彼长”究竟是怎么回事。
小红做一道四选项的选择题,我们把「选择题的正确答案」记作事件R,四个选项分别为A、B、C、D。
当小红没有任何信息来判断正确答案究竟是哪一个时,我们暂且认为小红觉得四个选项都有25%的概率成为正确答案(等概率情况),于是,事件R的熵便可根据公式计算如下:
S(R)=log24=2bit
这个时候,小红的朋友小橘向小红透露,选项A是正确答案的概率为40%,那么问题来了:
小红是否获得了该事件的「信息」?
如果小红获得了信息,那么它获得了多少信息?也就是说「信息量」是多少?
根据以上描述,我们认为小红得到小橘透露的消息之后,事件R的四个选项的概率变化了,选项A的概率为40%,选项B、C、D的概率分别为20%,这是不等概率的情况,我们同样可以计算这个时候事件R的熵:
S(R)=0.4∗log21/0.4+0.2∗log21/0.2+0.2∗log21/0.2+0.2∗log21/0.2=1.922bit
我们以此分析,小红得到小橘的消息之前,事件R的熵是2bit,而得到小橘的消息之后,事件R的熵是1.922bit,事件的熵减少了,于是我们判断:
小红通过小橘获得了该事件的「信息」,且获得的「信息量」为:2−1.922=0.078bit
尽管小红获得的信息量比较少,但不可否认,她获得了信息。紧接着,小红又通过另外一个朋友小黄,得知正确答案在C和D之间,于是事件R的四个选项的概率又变化了,选项A、B的概率分别为0%,现象C、D的概率分别为50%,这时事件R的熵为:
S(R)=0.5∗log21/0.5+0.5∗log21/0.5=1bit
聪明的你一定发现了,这不相当于抛硬币嘛?确实如此!我们据此知道小红从小黄那里得到了事件R的「信息」,且获得的「信息量」为:1.922−1=0.922bit
最后,小红最铁的一个朋友小黑直接把答案告诉她,就是选项C,至此,事件R从不确定事件变成了确定性事件,于是它的熵变为0了。我们据此知道小红从小黑那里得到了事件R的「信息」,且获得的「信息量」为:1−0=1bit
从以上例子中,我们可以总结出关于信息的几个特征:
信息的大小与传递它的方式无关,即与媒介无关,不管小橘、小黄、小黑是通过递纸条还是打电话,亦或是别的其他方式,都不影响信息的大小——信息量。不过需要注意的一点是,尽管信息量与媒介无关,但是媒介却影响信息转递的效率,古代传递信息需要邮差马匹,现在只需要通过微信发个短信即可,这个效率是天差地别的。
信息是相对的,这种相对性体现在三个方面:第一个是,信息是相对观察者而言的,同一个「消息」,对于不同的观察者而言对应的「信息量」不一定相同。比如上述例子中,小橘告诉小红的信息包含的信息量是0.078bit,而这个所谓的信息对于已经知道正确答案的小黑来说,不包含任何信息,信息量为0;第二个是,信息是相对于观察者对某个事件的了解程度而言的。在上述例子中,小红对事件R的不确定经历了几个变化,从一开始完全没有头绪,到后来小橘、小黄和小黑给她提供信息,我们计算信息量都是根据上一次小红对该事件的了解程度来计算熵差的。倘若小红没有经历小橘和小黄两个人的帮忙,直接跳到小黑给她正确答案这个环节,则小黑提供给她的信息量就不再是1bit,而是2−0=2bit;第三个是,信息是相对于事件而言的,同一个信息,如果对应的事件不同,则其包含的信息量也会有所不同。倘若小红所说的事件不是R,而是另外一道选择题L,那么小黑说正确答案是C,可能就提供不了任何信息量了。
信息是客观物理量。如何来理解这句话呢?信息用来消除事件的不确定性(即熵),它不会因为某个人说它消除了就消除了,说它没消除就没消除,需得经过客观的检验,才能知道它是否消除了事件的不确定性。就着这个话题稍微扯远一点便是:上述例子中,小橘所谓的「选项A的概率是40%」仅仅是我们为了辨析信息与熵所作的人为假设。在现实生活中,事件包含的各种情况的概率,尽管客观存在,但我们不是全能全知的上帝,我们所得到的概率,都是「统计学」意义上的概率,即根据众多的例子计算出来的一个对整体预估的结果。在这一点上,要格外抱有明确认知。
最后,再补充两个概念,这两个概念本可以在介绍「熵」时提出来,但为了让新学者先集中于「熵」,把它弄懂,避免众多概念对新学者的冲击,我们便把这两个概念放到最后,相信你弄懂了以上内容之后,再来理解这两个概念便轻松很多。
宏观态和微观态两个概念是两个不同视角下定义的。从整体来看,系统所处的状态便是宏观态;从内部来看,系统内部各个部分的不同分布状态,便是微观态。微观态构成了宏观态的不确定性(熵)。
我们小时候玩的搭积木游戏,所有的积木构成的整体便是宏观态,而积木处在不同位置拼搭出来的各种各样的形状,便是微观态。